【題目】如圖，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．
（1）求DE的長；
（2）求△ADB的面積．
【答案】解：（1）∵AD平分∠CAB，DE⊥AB，∠C=90°，
∴CD=DE，
∵CD="3" ，
∴DE=3；
（2）在Rt△ABC中，由勾股定理得：AB=AC+BC=6+8=10，∴AB=10，
∴△ADB的面積為S△ADB=
ABDE=
×10×3=15．
【解析】試題分析：（1）根據角平分線性質得出CD=DE，代入求出即可；
（2）利用勾股定理求出AB的長，然后計算△ADB的面積．
解：（1）∵AD平分∠CAB，DE⊥AB，∠C=90°，
∴CD=DE，
∵CD=3，
∴DE=3；
（2）在Rt△ABC中，由勾股定理得：AB=
=
=10，
∴△ADB的面積為S△ADB=
ABDE=×10×3=15．
名校課堂系列答案科目：初中數學 來源： 題型：
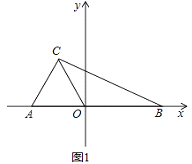
【題目】在平面直角坐標系中，A（a，0），B（b，0），C（﹣1，2）（見圖1），且 
（1）求a、b的值；
（2）①在x軸的正半軸上存在一點M，使三角形COM的面積是三角形ABC的面積的一半，求出點M的坐標；
②在坐標軸的其它位置是否存在點M，使三角形COM的面積三角形ABC的面積的一半仍然成立? 若存在，請直接寫出符合條件的點M的坐標；
（3）如圖2，過點C作CD⊥y軸交y軸于點D，點P為線段CD延長線上的一動點，連接OP，OE平分∠AOP，OF⊥OE．當點P運動時， 
的值是否會改變？若不變，求其值；若改變，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
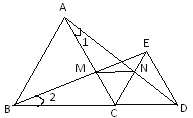
【題目】如圖，點C為線段BD上的點，分別以BC，CD為邊作等邊三角形ABC和等邊三角形ECD，連接BE交AC于點M，連接AD交CE于點N，連接MN.試說明：（1）
；（2）
為等邊三角形.
查看答案和解析>>
科目：初中數學 來源： 題型：
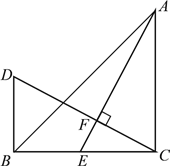
【題目】如圖，△ABC中，∠ACB＝90°，AC＝BC，AE是BC邊上的中線，過點C作CF⊥AE，垂足為F，過B作BD⊥BC交CF的延長線于D；若AC＝12cm，求BD的長；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）計算：（a－2）（a2＋2a＋4）＝ ，
（2x－y）（4x2＋2xy＋y2）＝ ．
（2）上面的整式乘法計算結果很簡單，由此又發現一個新的乘法公式： _________________________（請用含a、b的字母表示）
（3）下列各式能用你發現的乘法公式計算的是（ ）
A．（a－3）（a2－3a＋9） B．（2m－n）（2m2＋2mn＋n2）
C．（4－x）（16＋4x＋x2） D．（m－n）（m2＋2mn＋n2）
（4）直接用公式計算： 
=
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com