
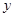 軸于點F,其中點E的橫坐標為-2,若直線
軸于點F,其中點E的橫坐標為-2,若直線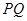 為拋物線的對稱軸,點G為直線
為拋物線的對稱軸,點G為直線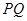 上的一動點,則
上的一動點,則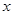 軸上是否存在一點H,使
軸上是否存在一點H,使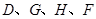 四點所圍成的四邊形周長最小,若存在,求出這個最小值及點G、H的坐標;若不存在,請說明理由;
四點所圍成的四邊形周長最小,若存在,求出這個最小值及點G、H的坐標;若不存在,請說明理由;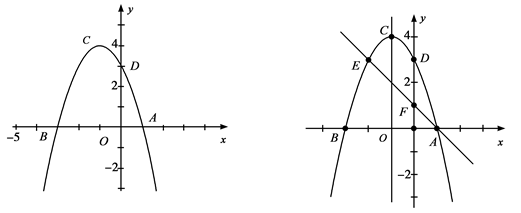

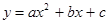 ,將A(1,0)、B(-3,0)、 D(0,3)代入,得
,將A(1,0)、B(-3,0)、 D(0,3)代入,得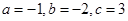 …………………………………………2分
…………………………………………2分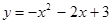 ……………………………3分
……………………………3分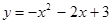 ,得
,得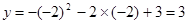
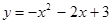 圖象分別與x軸、y軸交于點A(1,0)、B(-3,0)、
圖象分別與x軸、y軸交于點A(1,0)、B(-3,0)、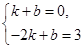 解得:
解得: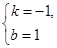
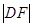 =2………………………………………③
=2………………………………………③ 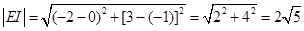 ……………………………………④
……………………………………④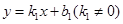 ,
,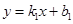 ,得:
,得: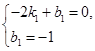 解得:
解得: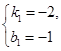
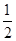 ;
; 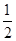 ,0)
,0)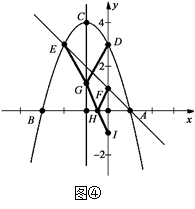
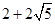
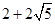 . …………………………………………7分
. …………………………………………7分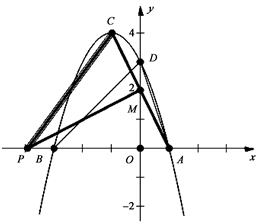
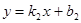 ,得:
,得: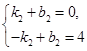
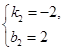 ,
,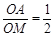 , ………………8分
, ………………8分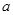 ,0),CM=
,0),CM=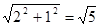 ,且∠CPM不可能為90°時,因此可分兩種情況討論; ……………………………………………………………………………9分
,且∠CPM不可能為90°時,因此可分兩種情況討論; ……………………………………………………………………………9分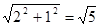 ,若
,若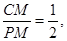 則
則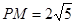 ,可求的P(-4,0),則CP=5,
,可求的P(-4,0),則CP=5,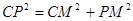 ,即P(-4,0)成立,若
,即P(-4,0)成立,若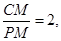 由圖可判斷不成立;……………………………………………………………………………………10分
由圖可判斷不成立;……………………………………………………………………………………10分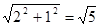 ,若
,若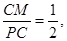 則
則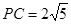 ,可求出
,可求出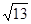 ,顯然不成立,若
,顯然不成立,若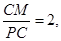 則
則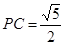 ,更不可能成立.……11分
,更不可能成立.……11分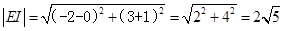 ,DF+EI=
,DF+EI=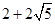
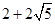 .
. 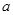 ,0),CM=
,0),CM=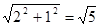 ,且∠CPM不可能為90°時,因此可分兩種情況討論,①當∠CMP=90°時,CM=
,且∠CPM不可能為90°時,因此可分兩種情況討論,①當∠CMP=90°時,CM=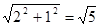 ,若
,若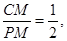 則
則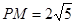 ,可求的P(-4,0),則CP=5,
,可求的P(-4,0),則CP=5,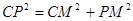 ,即P(-4,0)成立,若
,即P(-4,0)成立,若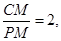 由圖可判斷不成立;②當∠PCM=90°時,CM=
由圖可判斷不成立;②當∠PCM=90°時,CM=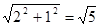 ,若
,若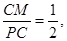 則
則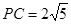 ,可求出P(-3,0),則PM=
,可求出P(-3,0),則PM=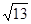 ,顯然不成立,若
,顯然不成立,若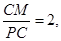 則
則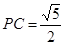 ,更不可能成立. 即求出以P、C、M為頂點的三角形與△AOM相似的P的坐標(-4,0)
,更不可能成立. 即求出以P、C、M為頂點的三角形與△AOM相似的P的坐標(-4,0) 

 步步高達標卷系列答案
步步高達標卷系列答案科目:初中數學 來源: 題型:
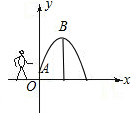 如圖,一小孩將一只皮球從A處拋出去,它所經過的路線是某個二次函數圖象的一部分,如果他的出手處A距地面的距離OA為1m,球路的最高點B(8,9),則這個二次函數的表達式為
如圖,一小孩將一只皮球從A處拋出去,它所經過的路線是某個二次函數圖象的一部分,如果他的出手處A距地面的距離OA為1m,球路的最高點B(8,9),則這個二次函數的表達式為查看答案和解析>>
科目:初中數學 來源: 題型:
如圖2,一小孩將一只皮球從A處拋出去,它所經過的路線是某個二次函數圖象的一部分,如果他的出手處A距地面的距離OA為1 m,球路的最高點B(8,9),則這個二次函數的表達式為______,小孩將球拋出了約______米(精確到0.1 m).
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2011屆河南省周口市初三下冊26章《二次函數》檢測題 題型:填空題
如圖2,一小孩將一只皮球從A處拋出去,它所經過的路線是某個二次函數圖象的一部分,如果他的出手處A距地面的距離OA為1 m,球路的最高點B(8,9),則這個二次函數的表達式為______,小孩將球拋出了約______米(精確到0.1 m).
查看答案和解析>>
科目:初中數學 來源:2010-2011學年河南省周口市初三下冊26章《二次函數》檢測題 題型:填空題
如圖2,一小孩將一只皮球從A處拋出去,它所經過的路線是某個二次函數圖象的一部分,如果他的出手處A距地面的距離OA為1 m,球路的最高點B(8,9),則這個二次函數的表達式為______,小孩將球拋出了約______米(精確到0.1 m).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com