
【題目】如圖,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于點D.
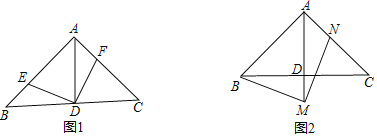
(1)如圖1,點E,F在AB,AC上,且∠EDF=90°.求證:BE=AF;
(2)點M,N分別在直線AD,AC上,且∠BMN=90°.如圖2,當點M在AD的延長線上時,求證:AB+AN=![]() AM;
AM;
【答案】(1)見解析;(2)見解析
【解析】
(1)先證∠BDE=∠ADF,再證△BDE≌△ADF,即可證明BE=AF;
(2)過點M作MP⊥AM,交AB的延長線于點P,先證△AMN≌△PMB,在Rt△AMP中,即可證明AB+AN=![]() AM.
AM.
解:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵AD⊥BC,
∴BD=CD,∠BAD=∠CAD=45°,
∴∠CAD=∠B,AD=BD,
∵∠EDF=∠ADC=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中
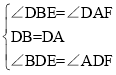
∴△BDE≌△ADF(ASA),
∴DE=DF;
(2)如圖,過點M作MP⊥AM,交AB的延長線于點P,
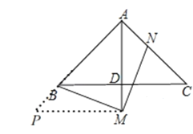
∴∠AMP=90°.
∵∠PAM=45°,
∴∠P=∠PAM=45°,
∴AM=PM.
∵∠BMN=∠AMP=90°,
∴∠BMP=∠AMN.
∵∠DAC=∠P=45°,
在△AMN和△PMB
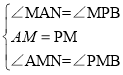
∴△AMN≌△PMB(ASA),
∴AN=PB,
∴AP=AB+BP=AB+AN,
在Rt△AMP中,∠AMP=90°,AM=MP,
∴AP=![]() AM,
AM,
∴AB+AN=![]() AM.
AM.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】為深入開展校園陽光一小時活動,九年級(1)班學生積極參與鍛煉,每位同學從籃球、跳繩、立定跳遠、長跑、鉛球中選一項進行鍛煉,訓練后都進行了測試.現將項目選擇情況及訓練后籃球定時定點投籃測試成績整理后作出如下統計圖:
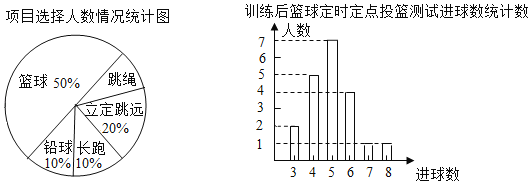
請你根據上面提供的信息回答下列問題:
(1)(扇形圖中)跳繩部分的扇形圓心角為 度,該班共有 人;訓練后,籃球定時定點投籃每個人進球數的平均數是 ,眾數是 ;
(2)老師決定從選擇跳繩訓練的3名女生和1名男生中任選兩名學生先進行測試,請用列表或畫樹形圖的方法求恰好選中兩名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在由邊長為1個單位長度的小正方形組成的網格圖中有格點△ABC(注:頂點在網格線交點處的三角形叫做格點三角形).只用沒有刻度的直尺,按如下要求畫圖,
(1)以點C為位似中心,在如圖中作△DEC∽ABC,且相似比為1:2;
(2)若點B為原點,點C(4,0),請在如圖中畫出平面直角坐標系,作出△ABC的外心,并直接寫出△ABC的外心的坐標
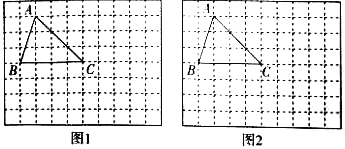
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】調查作業:了解你所住小區家庭3月份用氣量情況.
小天、小東和小蕓三位同學住在同一小區,該小區共有300戶家庭,每戶家庭人數在2—5之間,這300戶家庭的平均人數約為3.3.
小天、小東和小蕓各自對該小區家庭3月份用氣量情況進行了抽樣調查,將收集的數據進行了整理,繪制的統計表分別為表1、表2、表3,
表1抽樣調查小區4戶家庭3月份用氣量統計表(單位:![]() )
)
家庭人數 | 2 | 3 | 4 | 5 |
用氣量 | 14 | 19 | 21 | 26 |
表2抽樣調查小區15戶家庭3月份用氣量統計表(單位:![]() )
)
家庭人數 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用氣量 | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
表3抽樣調查小區15戶家庭3月份用氣量統計表(單位:![]() )
)
家庭人數 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用氣量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根據以上材料回答問題:
(1)小天、小東和小蕓三人中,哪一位同學抽樣調查的數據能較好地反應出該小區家庭3月份用氣量情況?請簡要說明其他兩位同學抽樣調查的不足之處;
(2)小東將表2中的數據按用氣量![]() 大小分為三類;
大小分為三類;
①節約型:![]() ;
;
②居中型:![]() ;
;
③偏高型:![]() ;并繪制成如下扇形統計圖,請幫助他將扇形圖補充完整;
;并繪制成如下扇形統計圖,請幫助他將扇形圖補充完整;
(3)小蕓算出表3中3月份平均每人的用量為![]() ,請估計該小區3月份的總用氣量.
,請估計該小區3月份的總用氣量.
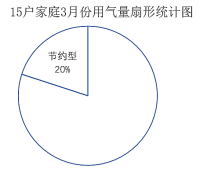
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數 y kx 與 y  的圖象交于 A、B 兩點,過 A 作 y 軸的垂線,交函數
的圖象交于 A、B 兩點,過 A 作 y 軸的垂線,交函數 的圖象于點 C,連接 BC,則△ABC 的面積為( )
的圖象于點 C,連接 BC,則△ABC 的面積為( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“煙花三月下揚州”-----揚州人杰地靈,是著名的旅游城市,繼獲“聯合國人居獎”后,2019年又獲“世界美食之都”的殊榮.“五一”長假期間,某餐飲企業為歡迎外地游客,推出了一個就餐酬賓活動:一只不透明的袋子中裝有分別標著A、B、C、D字母的四個球,分別對應揚州的四種美食:A--揚州醬菜、 B--揚州包子、C--揚州老鵝、D--揚州炒飯,這些球除字母標記外其余都相同.游客消費可參與活動:單筆消費滿600元可一次摸出一個球獲取一種相應的美食,單筆消費滿1000元可一次摸出兩個球獲取兩種相應的美食,單筆消費滿1300元可一次摸出三個球獲取三種相應的美食,單筆消費滿1500元可一次獲取四項獎品.某游客消費了1200元,參加這個活動,請用樹狀圖或列表的方式列出他獲得美食的所有可能結果,并求出獲得揚州包子和揚州老鵝的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】記某商品銷售單價為x元,商家銷售此種商品每月獲得的銷售利潤為y元,且y是關于x的二次函數.已知當商家將此種商品銷售單價分別定為55元或75元時,他每月均可獲得銷售利潤1800元;當商家將此種商品銷售單價定為80元時,他每月可獲得銷售利潤1550元,則y與x的函數關系式是( )
A.y=﹣(x﹣60)2+1825B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900D.y=﹣2(x﹣65)2+2000
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①表示一個時鐘的鐘面垂直固定于水平桌面上,其中分針上有一點A,當鐘面顯示3點30分時,分針垂直于桌面,A點距桌面的高度為10cm.圖②表示當鐘面顯示3點45分時,A點距桌面的高度為16cm,若鐘面顯示3點55分時,A點距桌面的高度為____![]() .
.
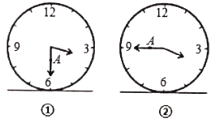
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+(4a﹣1)x﹣4與x軸交于點A、B,與y軸交于點C,且OC=2OB,點D為線段OB上一動點(不與點B重合),過點D作矩形DEFH,點H、F在拋物線上,點E在x軸上.
(1)求拋物線的解析式;
(2)當矩形DEFH的周長最大時,求矩形DEFH的面積;
(3)在(2)的條件下,矩形DEFH不動,將拋物線沿著x軸向左平移m個單位,拋物線與矩形DEFH的邊交于點M、N,連接M、N.若MN恰好平分矩形DEFH的面積,求m的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com