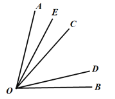
【題目】如圖，已知∠AOB=75°，∠COD=35°，∠COD在∠AOB的內部繞著點O旋轉(OC與OA不重合，OD與OB不重合)，若OE為∠AOC的角平分線．則2∠BOE－∠BOD的值為______．
科目：初中數學 來源： 題型：
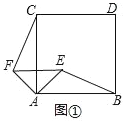
【題目】（1）如圖①，四邊形ABDC是正方形，以A為頂點，作等腰直角三角形△AEF，∠EAF=90°，線段BE與CF之間的數量關系為：_____．（直接寫出結果，不需要證明）
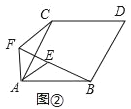
（2）如圖②，四邊形ABDC是菱形，以A為頂點，作等腰三角形△AEF，AE=AF，∠BAC=∠EAF，（1）中結論成立嗎？若成立，請證明；若不成立，請說明理由．
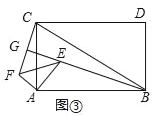
（3）如圖③，四邊形ABDC是矩形，以A為頂點，作直角三角形△AEF，∠EAF=90°，AB=
AC，AE=AF，當∠EAB=60°時，延長BE交CF于點G．
①求證：BE⊥CF；
②當AB=12，AE=4時，求線段BG的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
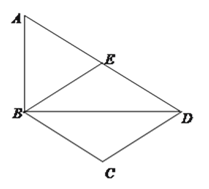
【題目】如圖，在Rt△ABD中，∠ABD=90°，AB=1，sin∠ADB=
，點E為AD的中點，線段BA繞點B順時針旋轉到BC（旋轉角小于180°），使BC∥AD．連接DC，BE．
（1）則四邊形BCDE是________，并證明你的結論；
（2）求線段AB旋轉過程中掃過的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】未成年人思想道德建設越來越受到社會的關注．某青少年研究機構隨機調查了某校 100名學生寒假花零花錢的數量（錢數取整數元），以便引導學生樹立正確的消費觀．根據調查 數據制成了如下的頻數分布表（部分空格未填）．
某校 100 名學生寒假花零花錢數量的頻數分布表:
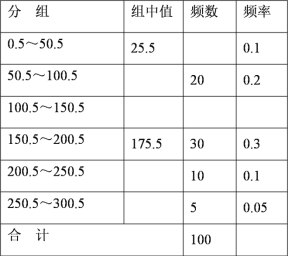
（1）完成該頻數分布表；
（2）畫出頻數分布直方圖．
（3）研究認為應對消費 150 元以上的學 生提出勤儉節約的建議．試估計應對該校1200 學生中約多少名學生提出該項建議？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】從泰州乘“K”字頭列車A、“T”字頭列車B都可直達南京，已知A車的平均速度為80 km/h，B車的平均速度為A車的1.5倍，且行完全程B車所需時間比A車少40分鐘．
(1)求泰州至南京的鐵路里程；
(2)若兩車以各自的平均速度分別從泰州、南京同時相向而行，問經過多少時間兩車相距40 km?
查看答案和解析>>
科目：初中數學 來源： 題型：
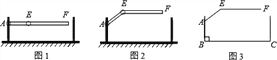
【題目】某地下車庫出口處安裝了“兩段式欄桿”，如圖1所示，點A是欄桿轉動的支點，點E是欄桿兩段的聯結點
當車輛經過時，欄桿AEF最多只能升起到如圖2所示的位置，其示意圖如圖3所示
欄桿寬度忽略不計
，其中
米，那么適合該地下車庫的車輛限高標志牌為
（參考數據：
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
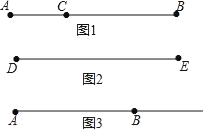
【題目】定義：若線段上的一個點把這條線段分成1：2的兩條線段，則稱這個點是這條線段的三等分點．如圖1，點C在線段AB上，且AC：CB＝1：2，則點C是線段AB的一個三等分點，顯然，一條線段的三等分點有兩個．
（1）已知：如圖2，DE＝15cm，點P是DE的三等分點，求DP的長．
（2）已知，線段AB＝15cm，如圖3，點P從點A出發以每秒1cm的速度在射線AB上向點B方向運動；點Q從點B出發，先向點A方向運動，當與點P重合后立馬改變方向與點P同向而行且速度始終為每秒2cm，設運動時間為t秒．
①若點P點Q同時出發，且當點P與點Q重合時，求t的值．
②若點P點Q同時出發，且當點P是線段AQ的三等分點時，求t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校計劃購買籃球、排球共20個，購買2個籃球，3個排球，共需花費190元；購買3個籃球的費用與購買5個排球的費用相同。
(1)籃球和排球的單價各是多少元?
(2)若購買籃球不少于8個，所需費用總額不超過800元.請你求出滿足要求的所有購買方案，并直接寫出其中最省錢的購買方案
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
