
【題目】已知數列{an}的前項n和為Sn , 且3Sn=4an﹣4.又數列{bn}滿足bn=log2a1+log2a2+…+log2an .
(1)求數列{an}、{bn}的通項公式;
(2)若 ![]() ,求使得不等式
,求使得不等式 ![]() 恒成立的實數k的取值范圍.
恒成立的實數k的取值范圍.
【答案】
(1)解:由3Sn=4an﹣4可得a1=4,
∵3Sn=4an﹣4,∴3Sn﹣1=4an﹣1﹣4,∴3Sn﹣3Sn﹣1=4an﹣4﹣(4an﹣1﹣4),
∴3an=4an﹣4an﹣1,即 ![]() .
.
∴數列{an}是首項為a1=4,公比為4的等比數列,∴ ![]() .
.
又bn=log2a1+log2a2+…+log2an=2+4+…+2(n﹣1)+2n=n(n+1),
∴bn=n(n+1)
(2)解: ![]() =1﹣
=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
不等式 ![]() 恒成立,即k≥
恒成立,即k≥ ![]() 恒成立,
恒成立,
設dn= ![]() ,則dn+1﹣dn=
,則dn+1﹣dn= ![]() ,
,
∴當n≥2時,數列{dn}單調遞減,當1≤n<2時,數列{dn}單調遞增;
即d1<d2>d3>d4>…,
∴數列最大項為 ![]() ,∴
,∴ ![]()
【解析】(1)利用再寫一式,兩式相減的方法求數列{an}的通項公式、利用數列{bn}滿足bn=log2a1+log2a2+…+log2an , 求出{bn}的通項公式;(2)若 ![]() ,裂項求和,不等式
,裂項求和,不等式 ![]() 恒成立,即k≥
恒成立,即k≥ ![]() 恒成立,即可實數k的取值范圍.
恒成立,即可實數k的取值范圍.
【考點精析】本題主要考查了數列的前n項和的相關知識點,需要掌握數列{an}的前n項和sn與通項an的關系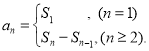 才能正確解答此題.
才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】某校![]() 屆高三文(1)班在一次數學測驗中,全班
屆高三文(1)班在一次數學測驗中,全班![]() 名學生的數學成績的頻率分布直方圖如下,已知分數在
名學生的數學成績的頻率分布直方圖如下,已知分數在![]() 的學生數有
的學生數有![]() 人.
人.
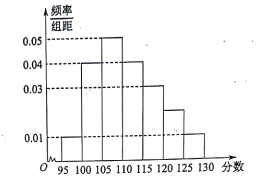
(1)求總人數![]() 和分數在
和分數在![]() 的人數
的人數![]() ;
;
(2)利用頻率分布直方圖,估算該班學生數學成績的眾數和中位數各是多少?
(3)現在從比分數在![]() 名學生(男女生比例為
名學生(男女生比例為![]() )中任選
)中任選![]() 人,求其中至多含有
人,求其中至多含有![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如下圖,在長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動,則直線D1E與A1D所成角的大小是 , 若D1E⊥EC,則直線A1D與平面D1DE所成的角為 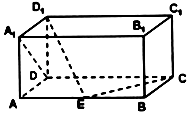
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=(ax﹣1)(x﹣1).
(1)若不等式f(x)<0的解集為{x|1<x<2},求實數a的值;
(2)當a>0時,解關于x的不等式f(x)<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】極坐標與參數方程
在直角坐標系![]() ,直線
,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).在以
為參數).在以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系中,曲線
軸正半軸為極軸建立極坐標系中,曲線![]() :
: ![]() .
.
(1)當![]() ,
, ![]() 時,判斷直線
時,判斷直線![]() 與曲線
與曲線![]() 的位置關系;
的位置關系;
(2)當![]() 時,若直線與曲
時,若直線與曲![]() 線
線![]() 相交于
相交于![]() ,
, ![]() 兩點,設
兩點,設![]() ,且
,且![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com