
【題目】如圖,在矩形ABCD中,點E是CD的中點,點F是BC上一點,且FC=2BF,連接AE,EF.若AB=2,AD=3,則tan∠AEF的值是_____.

 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2﹣6x+9與直線y=x+3交于A,B兩點(點A在點B的左側),拋物線的頂點為C,直線y=x+3與x軸交于點D.
(Ⅰ)求拋物線的頂點C的坐標及A,B兩點的坐標;
(Ⅱ)將拋物線y=x2﹣6x+9向上平移1個單位長度,再向左平移t(t>0)個單位長度得到新拋物線,若新拋物線的頂點E在△DAC內,求t的取值范圍;
(Ⅲ)點P(m,n)(﹣3<m<1)是拋物線y=x2﹣6x+9上一點,當△PAB的面積是△ABC面積的2倍時,求m,n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
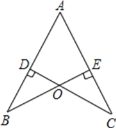
【題目】如圖,已知AB=AC,CD⊥AB于D,BE⊥AC于E,BE與CD相交于點O.
(1)問題探究:線段OB,OC有何數量關系,并說明理由;
(2)問題拓展:分別連接OA,BC,試判斷直線OA,BC的位置關系,并說明理由;
(3)問題延伸:將題目條件中的“CD⊥AB于D,BE⊥AC于E”換成“D、E分別為AB,AC邊上的中點”,(1)(2)中的結論還成立嗎?請直接寫出結論,不必說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 從
從![]() 開始沿折線
開始沿折線![]() 以
以![]() 的速度運動,點
的速度運動,點![]() 從
從![]() 開始沿
開始沿![]() 邊以
邊以![]() 的速度移動,如果點
的速度移動,如果點![]() 、
、![]() 分別從
分別從![]() 、
、![]() 同時出發,當其中一點到達
同時出發,當其中一點到達![]() 時,另一點也隨之停止運動,設運動時間為
時,另一點也隨之停止運動,設運動時間為![]() ,當
,當![]() ________時,四邊形
________時,四邊形![]() 也為矩形.
也為矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,BE=EC,將正方形ABCD的邊CD沿DE折疊到DF,連接EF、FC、FB,若△DFC的面積為16,則△BEF的面積為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,O是對角線AC與BD的交點,M是BC邊上的動點(點M不與B、C重合),過點C作CN垂直DM交AB于點N,連結OM、ON、MN.下列五個結論:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,則
;③ON⊥OM;④若AB=2,則![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正確結論是_________.(只填番號)
.其中正確結論是_________.(只填番號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c的頂點坐標為P(2,9),與x軸交于點A,B,與y軸交于點C(0,5).
(Ⅰ)求二次函數的解析式及點A,B的坐標;
(Ⅱ)設點Q在第一象限的拋物線上,若其關于原點的對稱點Q′也在拋物線上,求點Q的坐標;
(Ⅲ)若點M在拋物線上,點N在拋物線的對稱軸上,使得以A,C,M,N為頂點的四邊形是平行四邊形,且AC為其一邊,求點M,N的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“植樹節”期間,小王、小李兩人想通過摸球的方式來決定誰去參加學校植樹活動,規則如下:在兩個盒子內分別裝入標有數字1,2,3,4的四個和標有數字1,2,3的三個完全相同的小球,分別從兩個盒子中各摸出一個球,如果所摸出的球上的數字之和小于5,那么小王去,否則就是小李去.
(1)用樹狀圖或列表法求出小王去的概率;
(2)小李說:“這種規則不公平”,你認同他的說法嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com