【題目】甲乙兩個工程隊分別同時開挖兩條600米長的管道，所挖管道長度
（米）與挖掘時間
（天）之間的關系如圖所示，則下列說法中：
①甲隊每天挖100米；②乙隊開挖兩天后，每天挖50米；③甲隊比乙隊提前1天完成任務；④當
時，甲乙兩隊所挖管道長度相同，不正確的個數有（ ）
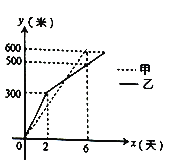
A. 4個B. 3個C. 2個D. 1個
【答案】D
【解析】
根據函數圖像中數據一次計算出各小題，從而可以解答本題.
①項，根據圖象可得，甲隊6天挖了600米，故甲隊每天挖：600÷6=100（米），故①項正確.
②項，根據圖象可知，乙隊前兩天共挖了300米，到第6天挖了500米，所以在6-2=4天內一共挖了：200（米），故開挖兩天后每天挖：200÷4=50（米），故②項正確.
③項，根據圖象可得，甲隊完成任務時間是6天，乙隊完成任務時間是：2+300÷50=8（天），故甲隊比乙隊提前8-6=2（天）完成任務，故③項錯誤；
④項，根據①，當x=4時，甲隊挖了：400（米），根據②，乙隊挖了：300+2×50=400（米），所以甲、乙兩隊所挖管道長度相同，故④項正確.
綜上所述，不正確的有③，共1個.
故本題正確答案為D.
科目：初中數學 來源： 題型：
【題目】如圖，OC在∠BOD內．
（1）如果∠AOC和∠BOD都是直角．
①若∠BOC=60°，則∠AOD的度數是 ；
②猜想∠BOC與∠AOD的數量關系，并說明理由；
（2）如果∠AOC=∠BOD=x°，∠AOD=y°，求∠BOC的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
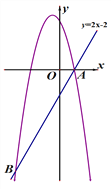
【題目】已知直線y=2x-2與拋物線
交于點A（1，0）和點B，且m＜n．
（1）當m=
時，直接寫出該拋物線頂點的坐標.
（2）求點B的坐標（用含m的代數式表示）.
（3）設拋物線頂點為C，記△ABC的面積為S.
①
，求線段AB長度的取值范圍；
②當
時，求對應的拋物線的函數表達式
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算：
（1）﹣28﹣（﹣15）+（﹣17）﹣（+5）
（2）（﹣72）×2
（3）
（4）
（5）3m2﹣mn﹣2m2+4mn
（6）（3x2﹣xy﹣2y2）﹣2（x2+xy﹣2y2）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為體現社會對教師的尊重，今年教師節出租節司機小王在東西方向的公路上免費接送教師，如果規定向東為正，向西為負，出租車的行程如下（單位：km）：
+15，-4，+13，-10，-12，+3，-13，-17
（1）最后一名教師被送到目的地時，小王在出發地的什么位置？
（2）若汽車耗油量為0.12L/km，小王出發前加滿了40L油，當他送完最后一名教師后，問他能否開車順利返回？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
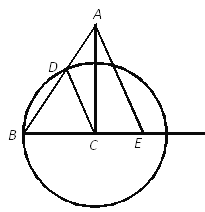
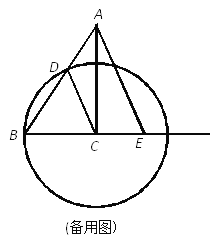
【題目】如圖，已知Rt△ABC 中，∠ACB=90°，BC=2，AC=3，以點C為圓心、CB為半徑的圓交AB于點D，過點A作AE∥CD，交BC延長線于點E.
（1）求CE的長；
（2）P是 CE延長線上一點，直線AP、CD交于點Q.
①如果△ACQ ∽△CPQ，求CP的長；
②如果以點A為圓心，AQ為半徑的圓與⊙C相切，求CP的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
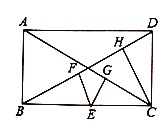
【題目】（1）如圖，已知矩形
中，點
是邊
上的一動點（不與點
、
重合），過點作
于點
，
于點
，
于點
，猜想線段
三者之間具有怎樣的數量關系，并證明你的猜想；
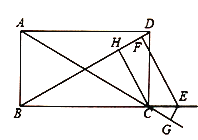
（2）如圖，若點在矩形的邊的延長線上，過點作于點，交
的延長線于點，于點，則線段三者之間具有怎樣的數量關系，直接寫出你的結論；
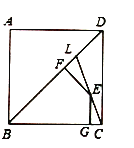
（3）如圖，
是正方形的對角線，
在上，且
，連接
，點是上任一點，與點，
于點，猜想線段
之間具有怎樣的數量關系，直接寫出你的猜想.
查看答案和解析>>
科目：初中數學 來源： 題型：
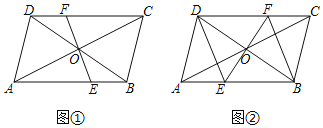
【題目】在ABCD中，對角線AC，BD相交于點O．EF過點O且與ABCD分別相交于點E，F
（1）如圖①，求證：OE=OF；
（2）如圖②，若EF⊥DB，垂足為O，求證：四邊形BEDF是菱形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，C為線段BD上一動點，分別過點B，D作AB⊥BD，ED⊥BD，連接AC，EC.已知AB＝5，DE＝2，BD＝12，設CD＝x.
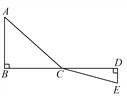
(1)用含x的代數式表示AC＋CE的長；
(2)請問點C在BD上什么位置時，AC＋CE的值最小？
(3)根據(2)中的規律和結論，請構圖求出代數式
的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com