
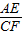 =
=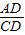 =
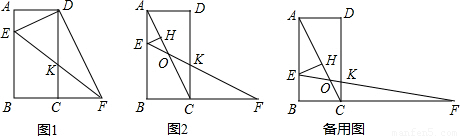
= ,∠DAE=∠DCF=90°,根據相似三角形的判定推出即可;
,∠DAE=∠DCF=90°,根據相似三角形的判定推出即可;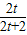 =
= ,求出即可;
,求出即可; ,得出AE=t,CF=2t,求出EM=
,得出AE=t,CF=2t,求出EM= t,證△MEO∽△CFO,得出
t,證△MEO∽△CFO,得出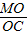 =
=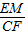 =
= ,求出MO=
,求出MO= CM,設HM=a,則EH=2a,AH=4a,求出MH=
CM,設HM=a,則EH=2a,AH=4a,求出MH= AM,推出OH=
AM,推出OH= AC,求出AC即可求出OH;②tan∠FOC的值是
AC,求出AC即可求出OH;②tan∠FOC的值是 或
或 ,理由是:根據△FKC∽△FEB求出KC=
,理由是:根據△FKC∽△FEB求出KC=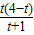 ,根據△CKO∽△AEO得出
,根據△CKO∽△AEO得出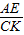 =
=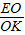 ,當
,當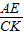 =
=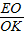 =
= 時得出
時得出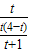 =2,求出t,即可得出AE長,根據△AEH∽△ACB,求出EH,當
=2,求出t,即可得出AE長,根據△AEH∽△ACB,求出EH,當 =
=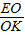 =
= 時得出
時得出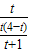 =
= ,求出t,根據△AEH∽△ACB,求出EH的值,解直角三角形求出即可.
,求出t,根據△AEH∽△ACB,求出EH的值,解直角三角形求出即可.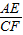 =
=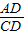 =
= ,
,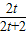 =
= ,
, ,
,
 t,
t,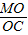 =
=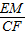 =
= ,
, OC,
OC, CM,
CM, AM,
AM, CM+
CM+ AM=
AM= AC,
AC,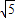 ,
, ,
,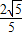 ;
; 或
或 ,
,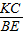 =
=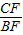 ,
,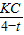 =
=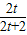 ,
, ,
,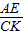 =
= ,
,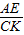 =
=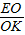 =
= 時,
時,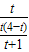 =2,
=2, ,
,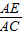 =
=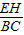 ,
,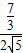 =
=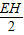 ,
,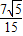 ,
, =
=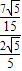 =
= ;
; =
=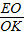 =
= 時,
時,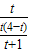 =
= ,
, ,
,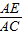 =
=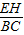 ,
,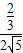 =
=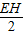 ,
,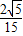 ,
,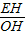 =
=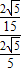 =
= .
.

科目:初中數學 來源: 題型:
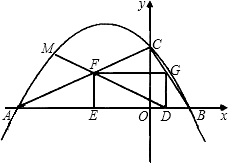 拋物線對稱軸為直線x=-3.
拋物線對稱軸為直線x=-3.| 2 | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:第6章《二次函數》常考題集(26):6.4 二次函數的應用(解析版) 題型:解答題
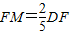 ,求出此時點M的坐標;
,求出此時點M的坐標;
查看答案和解析>>
科目:初中數學 來源:第23章《二次函數與反比例函數》常考題集(24):23.5 二次函數的應用(解析版) 題型:解答題
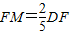 ,求出此時點M的坐標;
,求出此時點M的坐標;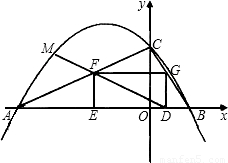
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com