
【題目】已知正方形ABCD的邊長為4,一個以點A為頂點的45°角繞點A旋轉,角的兩邊分別與邊BC、DC的延長線交于點E、F,連接EF.設CE=a,CF=b.
(1)如圖1,當∠EAF被對角線AC平分時,求a、b的值;
(2)當△AEF是直角三角形時,求a、b的值.
【答案】
(1)
解:∵四邊形ABCD是正方形,
∴∠BCF=∠DCE=90°
∵AC是正方形ABCD的對角線,
∴∠ACB=∠ACD=45°,
∴∠ACF=∠ACE,
∵∠EAF被對角線AC平分,
∴∠CAF=∠CAE,
在△ACF和△ACE中, 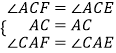 ,
,
∴△ACF≌△ACE,
∴CF=CE,
∵CE=a,CF=b,
∴a=b,
∵△ACF≌△ACE,
∴∠AEF=∠AFE,
∵∠EAF=45°,
∴∠AEF=∠AFE=67.5°,
∵CE=CF,∠ECF=90°,∠AEC=∠AFC=22.5°,
∵∠CAF=∠CAE=22.5°,
∴∠CAE=∠CEA,
∴CE=AC=4 ![]() ,即:a=b=4
,即:a=b=4 ![]()
(2)
解:當△AEF是直角三角形時,
①如圖所示:

∵∠AFE=90°,
∴∠AFD+∠CFE=90°,
∵∠CEF+∠CFE=90°,
∴∠AFD=∠CEF
∵∠AFE=90°,∠EAF=45°,
∴∠AEF=45°=∠EAF∴AF=EF,
在△ADF和△FCE中 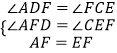 ,
,
∴△ADF≌△FCE,
∴FC=AD=4,CE=DF=CD+FC=8,
∴a=8,b=4.
②當∠AEF=90°時,同①的方法得,CF=4,CE=8,
∴a=4,b=8
【解析】(1)先證明△ACF≌△ACE,從而得到CF=CE,然后再證明△ACE為等腰三角形,則CE=AC=4 ![]() ;(2)當∠AFE=90°,可證明△ADF≌△FCE,則FC=AD=4,CE=DF=CD+FC=8,從而可求得a、b的值,同理當∠AEF=90°時,也可求得a、b的值.
;(2)當∠AFE=90°,可證明△ADF≌△FCE,則FC=AD=4,CE=DF=CD+FC=8,從而可求得a、b的值,同理當∠AEF=90°時,也可求得a、b的值.
【考點精析】本題主要考查了正方形的性質和旋轉的性質的相關知識點,需要掌握正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形;①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,D、E在AB上,且D、E分別是AC、BC的垂直平分線上一點.
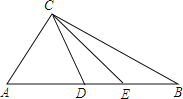
(1)若△CDE的周長為4,求AB的長;
(2)若∠ACB=100°,求∠DCE的度數;
(3)若∠ACB=a(90°<a<180°),則∠DCE=___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
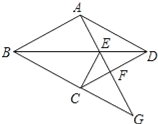
【題目】如圖,四邊形ABCD是菱形,點G是BC延長線上一點,連結AG,分別交BD、CD于點E、F,連結CE.
(1)求證:∠DAE=∠DCE;
(2)當CE=2EF時,EG與EF的等量關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,說明過程如下,請填上說明的依據:
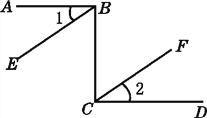
因為AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(______________),
所以∠ABC=∠BCD.
又因為∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF(______________).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國已有大概3.68億人參與“螞蟻森林種樹”活動,3.68億用科學記數法表示為( )
A.3.68×108B.3.68×107C.0.368×109D.36.8×107
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列語句是命題的個數( )
(1)延長線段AB,(2)兩條直線相交,只有一交點,(3)畫線段AB的中點,(4)若|x|=2,則x=2,(5)角平分線是一條射線.
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com