已知關于x的方程kx2+(3k+1)x+3=0.
(1)求證:無論k取任何實數時,方程總有實數根;
(2)若二次函數y=kx2+(3k+1)x+3的圖象與x軸兩個交點的橫坐標均為整數,且k為正整數,求k值;
(3)在(2)的條件下,設拋物線的頂點為M,直線y=-2x+9與y軸交于點C,與直線OM交于點D.現將拋物線平移,保持頂點在直線OD上.若平移的拋物線與射線CD(含端點C)只有一個公共點,求它的頂點橫坐標的值或取值范圍.
【答案】
分析:(1)分k=0時,方程為一元一次方程,有解,k≠0時,表示出根的判別式,再根據非負數的性質判斷出△≥0,得到一定有實數根;
(2)令y=0,解關于x一元二次方程,求出二次函數圖象與x軸的兩個交點的橫坐標都是整數求出k值為1;
(3)先根據(2)中的k值寫出二次函數解析式并整理成頂點式形式,然后寫出點P的坐標,然后寫出直線OP的解析式,再根據平移的性質設平移后的拋物線頂點坐標為(h,

h),然后寫出拋物線的頂點式形式為y=(x-h)
2+

h,再分①拋物線經過點C時,然后把點C的坐標代入拋物線求出h的值,再根據函數圖象寫出h的取值范圍;②直線與拋物線只有一個交點時,聯立直線與拋物線解析式消掉未知數y,利用根的判別式△=0列式求出h的值,然后求出交點坐標,從而得解.
解答:(1)證明:①當k=0時,方程為x+3=0,所以x=-3,方程有實數根,
②當k≠0時,△=(3k+1)
2-4k•3,
=9k
2+6k+1-12k,
=9k
2-6k+1,
=(3k-1)
2≥0,
所以,方程有實數根,
綜上所述,無論k取任何實數時,方程總有實數根;
(2)令y=0,則kx
2+(3k+1)x+3=0,
解關于x的一元二次方程,得x
1=-3,x
2=

,
∵二次函數的圖象與x軸兩個交點的橫坐標均為整數,且k為正整數,
∴k=1;
(3)由(2)得拋物線的解析式為y=x
2+4x+3,
配方得y=(x+2)
2-1,
∴拋物線的頂點M(-2,-1),
∴直線OD的解析式為y=

x,

于是設平移后的拋物線的頂點坐標為(h,

h),
∴平移后的拋物線解析式為y=(x-h)
2+

h,
①當拋物線經過點C時,令x=0,則y=9,
∴C(0,9),
∴h
2+

h=9,
解得h=
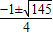
,
∴當
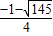
≤h<
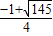
時,平移后的拋物線與射線CD只有一個公共點;
②當拋物線與直線CD只有一個公共點時,
由方程組
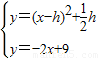
,
消掉y得,x
2+(-2h+2)x+h
2+

h-9=0,
∴△=(-2h+2)
2-4(h
2+

h-9)=0,
解得h=4,
此時拋物線y=(x-4)
2+2與射線CD唯一的公共點為(3,3),符合題意,
綜上所述:平移后的拋物線與射線CD只有一個公共點時,頂點橫坐標的值或取值范圍是h=4或
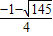
≤h<
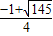
.
點評:本題是二次函數的綜合題型,主要考查了根的判別式,二次函數與x軸的交點問題,二次函數與不等式的關系,(3)根據CD是射線,要分情況討論.

 h),然后寫出拋物線的頂點式形式為y=(x-h)2+
h),然后寫出拋物線的頂點式形式為y=(x-h)2+ h,再分①拋物線經過點C時,然后把點C的坐標代入拋物線求出h的值,再根據函數圖象寫出h的取值范圍;②直線與拋物線只有一個交點時,聯立直線與拋物線解析式消掉未知數y,利用根的判別式△=0列式求出h的值,然后求出交點坐標,從而得解.
h,再分①拋物線經過點C時,然后把點C的坐標代入拋物線求出h的值,再根據函數圖象寫出h的取值范圍;②直線與拋物線只有一個交點時,聯立直線與拋物線解析式消掉未知數y,利用根的判別式△=0列式求出h的值,然后求出交點坐標,從而得解. ,
, x,
x,
 h),
h), h,
h, h=9,
h=9,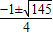 ,
,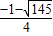 ≤h<
≤h<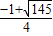 時,平移后的拋物線與射線CD只有一個公共點;
時,平移后的拋物線與射線CD只有一個公共點;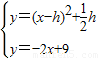 ,
, h-9=0,
h-9=0, h-9)=0,
h-9)=0,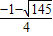 ≤h<
≤h<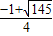 .
.

 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案 -kx-6=0的一個根為3,則實數k的值為(
)
-kx-6=0的一個根為3,則實數k的值為(
)