
如圖1是長方形紙袋,將紙袋沿EF折疊成圖2,再沿BF折疊成圖3,若∠DEF=α,用α表示圖3中∠CFE的大小為 _________ .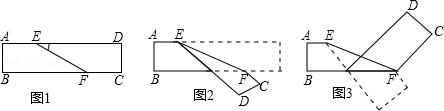
180°-3α.
解析試題分析:先根據進行的性質得AD∥BC,則∠BFE=∠DEF=α,根據折疊的性質,把如圖1中的方形紙袋沿EF折疊成圖2,則∠MEF=α,把圖2沿BF折疊成圖3,則∠MFH=∠CFM,根據平行線的性質由FH∥MG得到∠MFH=180°-∠FMG,再利用三角形外角性質得∠FMG=∠MFE+∠MEF=2α,則∠MFH=180°-2α,所以∠CFM=180°-2α,然后利用∠CFE=∠CFM-∠EFM求解.
試題解析:
在圖1中,
∵四邊形ABCD為矩形,
∴AD∥BC,
∴∠BFE=∠DEF=α,
∵如圖1中的方形紙袋沿EF折疊成圖2,
∴∠MEF=α,
∵圖2再沿BF折疊成圖3,
∴在圖3中,∠MFH=∠CFM,
∵FH∥MG,
∴∠MFH=180°-∠FMG,
∵∠FMG=∠MFE+∠MEF=α+α=2α,
∴∠MFH=180°-2α,
∴∠CFM=180°-2α,
∴∠CFE=∠CFM-∠EFM=180°-2α-α=180°-3α.
考點:翻折變換(折疊問題).


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com