
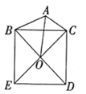
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為邊在
為邊在![]() 外作正方形
外作正方形![]() ,
,![]() 、
、![]() 交于點
交于點![]() ,則線段
,則線段![]() 的最大值為_______.
的最大值為_______.
【答案】![]()
【解析】
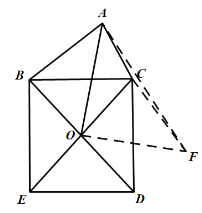
過O作OF⊥AO且使OF=AO,連接AF、CF,可知△AOF是等腰直角三角形,進而可得AF=![]() AO,根據(jù)正方形的性質(zhì)可得OB=OC,∠BOC=90°,進而可得∠AOB=∠COF,進而可得△AOB≌△COF,即可證明AB=CF,當(dāng)點A、C、F三點不共線時,根據(jù)三角形的三邊關(guān)系可得AC+CF>AF,當(dāng)點A、C、F三點共線時可得AC+CF=AC+AB=AF=6,即可得AF的最大值,由AF=
AO,根據(jù)正方形的性質(zhì)可得OB=OC,∠BOC=90°,進而可得∠AOB=∠COF,進而可得△AOB≌△COF,即可證明AB=CF,當(dāng)點A、C、F三點不共線時,根據(jù)三角形的三邊關(guān)系可得AC+CF>AF,當(dāng)點A、C、F三點共線時可得AC+CF=AC+AB=AF=6,即可得AF的最大值,由AF=![]() AO即可得答案.
AO即可得答案.
如圖,過O作OF⊥AO且使OF=AO,連接AF、CF,
∴∠AOF=90°,△AOF是等腰直角三角形,
∴AF=![]() AO,
AO,
∵四邊形BCDE是正方形,
∴OB=OC,∠BOC=90°,
∵∠BOC=∠AOF=90°,
∴∠AOB+∠AOC=∠COF+∠AOC,
∴∠AOB=∠COF,
又∵OB=OC,AO=OF,
∴△AOB≌△COF,
∴CF=AB=4,
當(dāng)點A、C、F三點不共線時,AC+CF>AF,
當(dāng)點A、C、F三點共線時,AC+CF=AC+AB=AF=6,
∴AF≤AC+CF=6,
∴AF的最大值是6,
∴AF=![]() AO=6,
AO=6,
∴AO=![]() .
.
故答案為:![]()


科目:初中數(shù)學(xué) 來源: 題型:
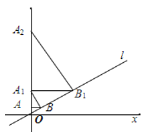
【題目】如圖,已知直線l:y=![]() x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;……按此作法繼續(xù)下去,則點A2020的坐標(biāo)為______________.
x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;……按此作法繼續(xù)下去,則點A2020的坐標(biāo)為______________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
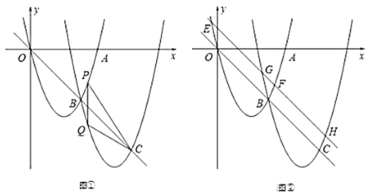
【題目】如圖①,拋物線![]() 交
交![]() 正半軸于點
正半軸于點![]() ,將拋物線
,將拋物線![]() 先向右平移
先向右平移![]() 個單位,再向下平移
個單位,再向下平移![]() 個單位得到拋物線
個單位得到拋物線![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() .
.
(1)求拋物線![]() 的解析式;
的解析式;
(2)點![]() 是拋物線
是拋物線![]() 上
上![]() (含端點)間的一點,作
(含端點)間的一點,作![]() 軸交拋物線
軸交拋物線![]() 于點
于點![]() ,連按
,連按![]() ,
,![]() .當(dāng)
.當(dāng)![]() 的面積為
的面積為![]() 時, 求點
時, 求點![]() 的坐標(biāo);
的坐標(biāo);
(3)如圖②,將直線![]() 向上平移,交拋物線
向上平移,交拋物線![]() 于點
于點![]() 、
、![]() ,交拋物線
,交拋物線![]() 于點
于點![]() 、
、![]() ,試判斷
,試判斷![]() 的值是否為定值,并說明理由.
的值是否為定值,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸的交點
軸的交點![]() 在點
在點![]() 與點
與點![]() 之間(不包括這兩點),對稱軸為直線
之間(不包括這兩點),對稱軸為直線![]() .有下列結(jié)論:
.有下列結(jié)論:
①![]() ;②
;②![]() ;③
;③![]() ;④若點
;④若點![]() ,
,![]() 在拋物線上,則
在拋物線上,則![]() .其中正確結(jié)論的個數(shù)是()
.其中正確結(jié)論的個數(shù)是()
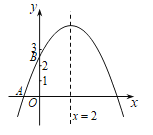
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
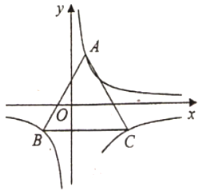
【題目】如圖,等邊三角形![]() 的頂點
的頂點![]() ,
,![]() 分別在反比例函數(shù)
分別在反比例函數(shù)![]()
![]() 圖象的兩個分支上,點
圖象的兩個分支上,點![]() 在反比例函數(shù)
在反比例函數(shù)![]() 的圖象上,
的圖象上,![]() 軸.當(dāng)
軸.當(dāng)![]() 的面積最小時,
的面積最小時,![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】問題探究
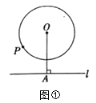
(1)如圖①,已知![]() 與直線
與直線![]() ,過
,過![]() 作
作![]() 于點
于點![]() ,
,![]() ,
,![]() 的半徑為
的半徑為![]() ,則圓上一點
,則圓上一點![]() 到
到![]() 的距離的最小值是______;
的距離的最小值是______;
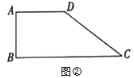
(2)如圖②,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,過點
,過點![]() 作一條直線交邊
作一條直線交邊![]() 或
或![]() 于
于![]() ,若
,若![]() 平分四邊形
平分四邊形![]() 的面積,求
的面積,求![]() 的長;
的長;
問題解決
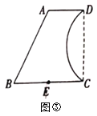
(3)如圖③所示,是由線段![]() 、
、![]() 、
、![]() 與弧
與弧![]() 圍成的花園的平面示意圖,
圍成的花園的平面示意圖,![]() ,
,![]() ,
,![]() //
//![]() ,CD⊥BC,點
,CD⊥BC,點![]() 為
為![]() 的中點,
的中點,![]() 所對的圓心角為
所對的圓心角為![]() .管理人員想在
.管理人員想在![]() 上確定一點
上確定一點![]() ,在四邊形
,在四邊形![]() 區(qū)域種植花卉,其余區(qū)域種植草坪,并過
區(qū)域種植花卉,其余區(qū)域種植草坪,并過![]() 點修建一條小路
點修建一條小路![]() ,把四邊形
,把四邊形![]() 分成面積相等且盡可能小的兩部分,分別種植不同的花卉.問是否存在滿足上述條件的小路
分成面積相等且盡可能小的兩部分,分別種植不同的花卉.問是否存在滿足上述條件的小路![]() ?若存在,請求出
?若存在,請求出![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 的圖象與
的圖象與![]() 軸的交點坐標(biāo)為
軸的交點坐標(biāo)為![]() 和
和![]() .
.
(1)求![]() 和
和![]() (用
(用![]() 的代數(shù)式表示);
的代數(shù)式表示);
(2)若在自變量![]() 的值滿足
的值滿足![]() 的情況下,與其對應(yīng)的函數(shù)值
的情況下,與其對應(yīng)的函數(shù)值![]() 的最大值為1,求
的最大值為1,求![]() 的值;
的值;
(3)已知點![]() 和點
和點![]() .若二次函數(shù)
.若二次函數(shù)![]() 的圖象與線段
的圖象與線段![]() 有兩個不同的交點,直接寫出
有兩個不同的交點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)![]() :
:![]() 和二次函數(shù)
和二次函數(shù)![]() :
:![]()
![]() 圖象的頂點分別為
圖象的頂點分別為![]() 、
、![]() ,與
,與![]() 軸分別相交于
軸分別相交于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左邊)和
的左邊)和![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左邊),
的左邊),
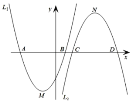
(1)函數(shù)![]() 的頂點坐標(biāo)為______;當(dāng)二次函數(shù)
的頂點坐標(biāo)為______;當(dāng)二次函數(shù)![]() ,
,![]() 的
的![]() 值同時隨著
值同時隨著![]() 的增大而增大時,則
的增大而增大時,則![]() 的取值范圍是_______;
的取值范圍是_______;
(2)判斷四邊形![]() 的形狀(直接寫出,不必證明);
的形狀(直接寫出,不必證明);
(3)拋物線![]() ,
,![]() 均會分別經(jīng)過某些定點;
均會分別經(jīng)過某些定點;
①求所有定點的坐標(biāo);
②若拋物線![]() 位置固定不變,通過平移拋物線
位置固定不變,通過平移拋物線![]() 的位置使這些定點組成的圖形為菱形,則拋物線
的位置使這些定點組成的圖形為菱形,則拋物線![]() 應(yīng)平移的距離是多少?
應(yīng)平移的距離是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
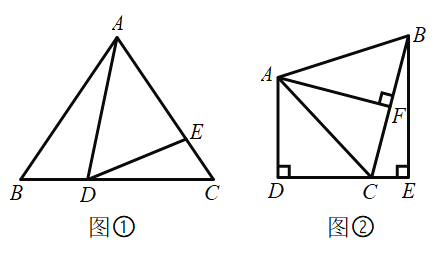
【題目】如圖①,在![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的點,且
上的點,且![]() .
.
(1)若![]() ,
,![]() ,設(shè)
,設(shè)![]() ,
,![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)如圖②,![]() ,
,![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,點
,點![]() 在線段
在線段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com