
【題目】“壯麗70載,奮進新時代”.值偉大祖國70華誕之際,某網店特別推出甲、乙兩種紀念文化衫,已知甲種紀念文化衫的售價比乙種紀念文化衫多15元,廣益中學陳老師從該網店購買了2件甲種紀念文化衫和3件乙種紀念文化衫,共花費255元.
(1)該網店甲、乙兩種紀念文化衫每件的售價各是多少元?
(2)根據消費者需求,該網店決定用不超過8780元購進甲、乙兩種紀念文化衫共200件,且甲種紀念文化衫的數量大于乙種紀念文化衫數量的![]() ,已知甲種紀念文化衫每件的進價為50元,乙種紀念文化衫每件的進價為40元.
,已知甲種紀念文化衫每件的進價為50元,乙種紀念文化衫每件的進價為40元.
①若設購進甲種紀念文化衫m件,則該網店有哪幾種進貨方案?
②若所購進紀念文化衫均可全部售出,請求出網店所獲利潤W(元)與甲種紀念文化衫進貨量m(件)之間的函數關系式,并說明當m為何值時所獲利潤最大?最大利潤是多少?
【答案】(1)甲種紀念文化衫每件的售價是60元,乙種紀念文化衫每件的售價是45元;(2)①進貨方案有三種,分別為:方案一:購進甲種紀念文化衫76件,則乙種紀念文化衫為124件;方案二:購進甲種紀念文化衫77件,則乙種紀念文化衫為123件;方案三:購進甲種紀念文化衫78件,則乙種紀念文化衫為122件;②W=5m+1000,當m=78時,所獲利潤最大,最大利潤為1390元.
【解析】
(1)設甲種紀念文化衫每件的售價是x元,乙種紀念文化衫每件的售價是y元,由題意,列二元一次方程組,求解即可;(2)①若購進甲種紀念文化衫m件,則乙種紀念文化衫為(200m)件,由題意得一元一次不等式組,求解,并根據m為整數,可求得m的值,即可得進貨方案;②用含m的式子表示出W,根據一次函數的性質可得答案.
解:(1)設甲種紀念文化衫每件的售價是x元,乙種紀念文化衫每件的售價是y元,由題意得:
![]()
解得:![]()
答:甲種紀念文化衫每件的售價是60元,乙種紀念文化衫每件的售價是45元.
(2)①若購進甲種紀念文化衫m件,則乙種紀念文化衫為(200﹣m)件,
由題意得:
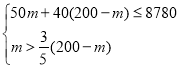
解得:75<m≤78
∵m為整數
∴m的值為:76,77,78.
進貨方案有三種,分別為:
方案一:購進甲種紀念文化衫76件,則乙種紀念文化衫為124件;
方案二:購進甲種紀念文化衫77件,則乙種紀念文化衫為123件;
方案三:購進甲種紀念文化衫78件,則乙種紀念文化衫為122件.
②由題意得:
W=(60﹣50)m+(45﹣40)(200﹣m)=5m+1000
∵5>0
∴W隨m的增大而增大,且75<m≤78
∴當m=78時,W最大,W的最大值為:5×78+1000=1390元.
答:②當m=78時,所獲利潤最大,最大利潤為1390元.


 互動英語系列答案
互動英語系列答案科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() 兩點.
兩點.
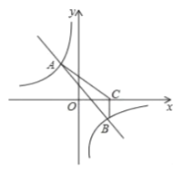
(1)求一次函數與反比例函數的解析式;
(2)根據已知條件,請直接寫出不等式![]() 的解集;
的解集;
(3)過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
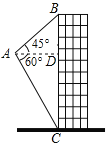
【題目】如圖,航拍無人機從A處測得一幢建筑物頂部B的仰角為45°,測得底部C的角為60°,此時航拍無人機與該建筑物的水平距離AD為80m,那么該建筑物的高度BC為_____m(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
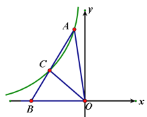
【題目】如圖,在△AOB中,OC平分∠AOB,![]() ,反比例函數
,反比例函數![]() 圖像經過點A、C兩點,點B在x軸上,若△AOB的面積為7,則k的值為( )
圖像經過點A、C兩點,點B在x軸上,若△AOB的面積為7,則k的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
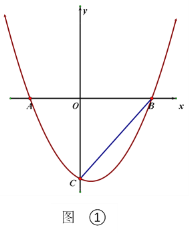
【題目】如圖,拋物線![]() 交x軸于A、B兩點(點A在點B的左側),
交x軸于A、B兩點(點A在點B的左側),![]() .
.
(1)求拋物線的函數表達式;
(2)如圖①,連接BC,點P在拋物線上,且∠BCO=![]() ∠PBA.求點P的坐標
∠PBA.求點P的坐標
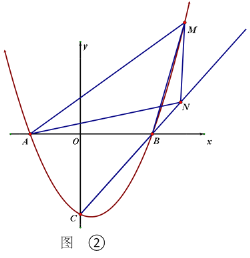
(3)如圖②,M是拋物線上一點,N為射線CB上的一點,且M、N兩點均在第一象限內,B、N是位于直線AM同側的不同兩點,![]() ,點M到
,點M到![]() 軸的距離為2L,△AMN的面積為5L,且∠ANB=∠MBN,請問MN的長是否為定值?如果是,請求出這個定值;如果不是,請說明理由.
軸的距離為2L,△AMN的面積為5L,且∠ANB=∠MBN,請問MN的長是否為定值?如果是,請求出這個定值;如果不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,點 A 是直線 l 上的一點.
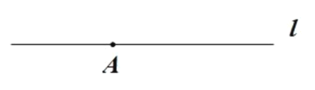
求作:正方形 ABCD,使得點 B 在直線 l 上.(要求保留作圖痕跡,不用寫作法) 請你說明,∠BAD=90°的依據是什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 是
是![]() 邊上的中線,點
邊上的中線,點![]() 是
是![]() 的中點,過點
的中點,過點![]() 作
作![]() 交
交![]() 的延長線于
的延長線于![]() ,
,![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
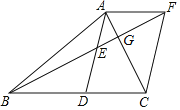
(1)求證:![]() ;
;
(2)若![]() ,①試判斷四邊形
,①試判斷四邊形![]() 的形狀,并證明你的結論;
的形狀,并證明你的結論;
②若![]() ,
,![]() ,直接寫出線段
,直接寫出線段![]() 的長_________.
的長_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為倡導節能環保,降低能源消耗,提倡環保型新能源開發,造福社會.某公司研發生產一種新型智能環保節能燈,成本為每件40元.市場調查發現,該智能環保節能燈每件售價y(元)與每天的銷售量為x(件)的關系如圖,為推廣新產品,公司要求每天的銷售量不少于1000件,每件利潤不低于5元.
(1)求每件銷售單價y(元)與每天的銷售量為x(件)的函數關系式并直接寫出自變量x的取值范圍;
(2)設該公司日銷售利潤為P元,求每天的最大銷售利潤是多少元?
(3)在試銷售過程中,受國家政策扶持,毎銷售一件該智能環保節能燈國家給予公司補貼m(m≤40)元.在獲得國家每件m元補貼后,公司的日銷售利潤隨日銷售量的增大而增大,則m的取值范圍是 (直接寫出結果).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com