
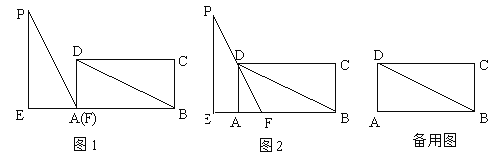
【題目】如圖1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(點F和點A重合)的邊EF和矩形的邊AB在同一直線上.現將Rt△PEF從A以每秒1個單位的速度向射線AB方向勻速平移,當點F與點B重合時停止運動,設運動時間為t秒,
解答下列問題:
(1)如圖1,連接PD,填空:∠PFD= ,四邊形PEAD的面積是 ;
(2)如圖2,當PF經過點D時,求 △PEF運動時間t的值;
(3)在運動的過程中,設△PEF與△ABD重疊部分面積為S,請求出S與t的函數關系式.
【答案】(1)300,![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】(1)根據銳角三角形函數可求出角的度數,然后根據勾股定理求出PE的長,再根據梯形的面積公式求解.
(2)當PF經過點D時,PE∥DA,由EF=3,PF=6,可得∠EPD=∠ADF=30°,用三角函數計算可得AF=t=![]() ;
;
(3)根據題意,分三種情況:①當0≤t<![]() 時,②
時,②![]() ≤t<3時,③3≤t≤6時,根據三角形、梯形的面積的求法,求出S與t的函數關系式即可.
≤t<3時,③3≤t≤6時,根據三角形、梯形的面積的求法,求出S與t的函數關系式即可.
(1)∵在Rt△PEF中,∠PEF=90°,EF=3,PF=6
∴sin∠P=![]()
∴∠P=30°
∵PE∥AD
∴∠PAD=300,
根據勾股定理可得PE=3![]() ,
,
所以S四邊形PEAD=![]() ×(3
×(3![]() +3)×3=
+3)×3=![]() ;
;
(2)當PF經過點D時,PE∥DA,由EF=3,PF=6,得∠EPF=∠ADF=30°,
在Rt△ADF中,由AD=3,得AF=![]() ,所以t=
,所以t=![]() ;
;
(3)分三種情況討論:
①當0≤t<![]() 時, PF交AD于Q,∵AF=t,AQ=
時, PF交AD于Q,∵AF=t,AQ=![]() t,∴S=
t,∴S=![]() ×t×
×t×![]() t=
t=![]() ;
;
②當![]() ≤t<3時,PF交BD于K,作KH⊥AB于H,∵AF=t,∴BF=3
≤t<3時,PF交BD于K,作KH⊥AB于H,∵AF=t,∴BF=3![]() -t,S△ABD=
-t,S△ABD=![]() ,
,
∵∠FBK=∠FKB,∴FB=FK=3![]() -t,KH=KF×sin600=
-t,KH=KF×sin600=![]() ,∴S=S△ABD﹣S△FBK =
,∴S=S△ABD﹣S△FBK =![]()
③當3≤t≤3![]() 時,PE與BD交O,PF交BD于K,∵AF=t,∴AE=t-3,BF=3
時,PE與BD交O,PF交BD于K,∵AF=t,∴AE=t-3,BF=3![]() -t,
-t,
BE=3![]() -t+3,OE=BE×tan300=
-t+3,OE=BE×tan300=![]() ,∴S=
,∴S=![]() 。
。


科目:初中數學 來源: 題型:
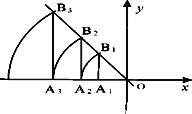
【題目】如圖,直線l:y=-![]() x,點A1坐標為(-4,0).過點A1作x軸的垂線交直線l于點B1,以原點O為圓心,OB1長為半徑畫弧交x軸負半軸于點A2,再過點A2作x軸的垂線交直線l于點B2,以原點O為圓心,OB2長為半徑畫弧交x軸負半軸于點A3,…,按此做法進行下去,點A2018的坐標為_______.
x,點A1坐標為(-4,0).過點A1作x軸的垂線交直線l于點B1,以原點O為圓心,OB1長為半徑畫弧交x軸負半軸于點A2,再過點A2作x軸的垂線交直線l于點B2,以原點O為圓心,OB2長為半徑畫弧交x軸負半軸于點A3,…,按此做法進行下去,點A2018的坐標為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 表示5與-2之差的絕對值,實際上也可理解為5與-2兩數在數軸上所對應的兩點之間的距離請試著探索:
表示5與-2之差的絕對值,實際上也可理解為5與-2兩數在數軸上所對應的兩點之間的距離請試著探索:
(1)找出所有符合條件的整數![]() ,使
,使![]() ,這樣的整數是__________;
,這樣的整數是__________;
(2)利用數軸找出,當![]() 時,
時,![]() 的值是__________;
的值是__________;
(3)利用數軸找出,當![]() 取最小值時,
取最小值時,![]() 的范圍是__________.
的范圍是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學七年級開展演講比賽,學校決定購買一些筆記本和鋼筆作為獎品.現了解情況如下:甲、乙兩家商店出售兩種同樣品牌的筆記本和鋼筆.筆記本定價為每本20元,鋼筆每支定價5元,經洽談后,甲店每買一本筆記本贈一支鋼筆;乙店全部按定價的9折優惠.七年級需筆記本20本,鋼筆若干支(不小于20支).問:
(1)如果購買鋼筆![]() (
(![]() 不小于20)支,則在甲店購買需付款 ______ 元,在乙店購買需付款 _______________ 元.(用x的代數式表示)
不小于20)支,則在甲店購買需付款 ______ 元,在乙店購買需付款 _______________ 元.(用x的代數式表示)
(2)當購買鋼筆多少支時,在兩店購買付款一樣?
查看答案和解析>>
科目:初中數學 來源: 題型:
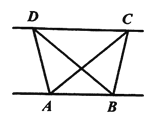
【題目】(1)探究新知:如圖1,已知![]() 與
與![]() 的面積相等,試判斷
的面積相等,試判斷![]() 與
與![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
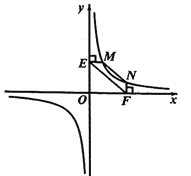
(2)結論應用:
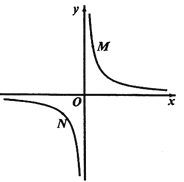
①如圖2,點![]() ,
,![]() 在反比例函數
在反比例函數![]() 的圖像上,過點
的圖像上,過點![]() 作
作![]() 軸,過點
軸,過點![]() 作
作![]() 軸,垂足分別為
軸,垂足分別為![]() ,
,![]() ,連接
,連接![]() .試證明:
.試證明:![]() .
.
②若①中的其他條件不變,只改變點![]() ,
,![]() 的位置如圖3所示,請畫出圖形,判斷
的位置如圖3所示,請畫出圖形,判斷![]() 與
與![]() 的位置關系并說明理由.
的位置關系并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《教育導報》記者就四川省農村中小學教師閱讀狀況進行了一次問卷調查,并根據調查結果繪制了教師每年閱讀書籍數量的統計圖(不完整).設x表示閱讀書籍的數量(x為正整數,單位:本).其中A:1≤x≤3; B:4≤x≤6; C:7≤x≤9;D:x≥10.請你根據兩幅圖提供的信息解答下列問題:
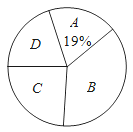
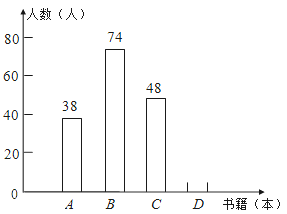
(1)本次共調查了多少名教師?
(2)補全條形統計圖;
(3)計算扇形統計圖中扇形D的圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】書店舉行購書優惠活動:
①一次性購書不超過100元,不享受打折優惠;
②一次性購書超過100元但不超過200元,一律按原價打九折;
③一次性購書超過200元,一律按原價打七折.
小麗在這次活動中,兩次購書總共付款229.4元,第二次購書原價是第一次購書原價的3倍,那么小麗這兩次購書原價的總和是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個有進水管與出水管的容器,從某時刻開始的4分內只進水不出水,在隨后的若干分內既進水又出水,之后只有出水不進水,每分鐘的進水量和出水量是兩個常數,容器內的水量![]() (單位:升)與時間
(單位:升)與時間![]() (單位:分)之間的關系如圖所示,則進水速度是______升/分,出水速度是______升/分,
(單位:分)之間的關系如圖所示,則進水速度是______升/分,出水速度是______升/分,![]() 的值為______.
的值為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com