
【題目】已知:關于x的方程![]()
(1)求證:m取任何值時,方程總有實根.
(2)若二次函數![]() 的圖像關于y軸對稱.
的圖像關于y軸對稱.
a、求二次函數![]() 的解析式
的解析式
b、已知一次函數![]() ,證明:在實數范圍內,對于同一x值,這兩個函數所對應的函數值
,證明:在實數范圍內,對于同一x值,這兩個函數所對應的函數值![]() 均成立.
均成立.
(3)在(2)的條件下,若二次函數![]() 的象經過(-5,0),且在實數范圍內,對于x的同一個值,這三個函數所對應的函數值
的象經過(-5,0),且在實數范圍內,對于x的同一個值,這三個函數所對應的函數值![]() 均成立,求二次函數
均成立,求二次函數![]() 的解析式.
的解析式.
【答案】(1)證明見解析;(2)a、y1=x2-1;b、證明見解析;(3)![]() .
.
【解析】
(1)首先此題的方程并沒有明確是一次方程還是二次方程,所以要分類討論:
①m=0,此時方程為一元一次方程,經計算可知一定有實數根;
②m≠0,此時方程為二元一次方程,可表示出方程的根的判別式,然后結合非負數的性質進行證明.
(2)①由于拋物線的圖象關于y軸對稱,那么拋物線的一次項系數必為0,可據此求出m的值,從而確定函數的解析式;
②此題可用作差法求解,令y1-y2,然后綜合運用完全平方式和非負數的性質進行證明.
(3)根據②的結論,易知y1、y2的交點為(1,0),由于y1≥y3≥y2成立,即三個函數都交于(1,0),結合點(-5,0)的坐標,可用a表示出y3的函數解析式;已知y3≥y2,可用作差法求解,令y=y3-y2,可得到y的表達式,由于y3≥y2,所以y≥0,可據此求出a的值,即可得到拋物線的解析式.
解:(1)分兩種情況:
當m=0時,原方程可化為3x-3=0,即x=1; ∴m=0時,原方程有實數根;
當m≠0時,原方程為關于x的一元二次方程,
∵△=[-3(m-1)]2-4m(2m-3)=m2-6m+9=(m-3)2≥0,
∴方程有兩個實數根;
綜上可知:m取任何實數時,方程總有實數根;
(2)①∵關于x的二次函數y1=mx2-3(m-1)x+2m-3的圖象關于y軸對稱;
∴3(m-1)=0,即m=1;
∴拋物線的解析式為:y1=x2-1;
②∵y1-y2=x2-1-(2x-2)=(x-1)2≥0,
∴y1≥y2(當且僅當x=1時,等號成立);
(3)由②知,當x=1時,y1=y2=0,即y1、y2的圖象都經過(1,0);
∵對應x的同一個值,y1≥y3≥y2成立,
∴y3=ax2+bx+c的圖象必經過(1,0),
又∵y3=ax2+bx+c經過(-5,0),
∴y3=a(x-1)(x+5)=ax2+4ax-5a;
設y=y3-y2=ax2+4ax-5a-(2x-2)=ax2+(4a-2)x+(2-5a);
對于x的同一個值,這三個函數對應的函數值y1≥y3≥y2成立,
∴y3-y2≥0,
∴y=ax2+(4a-2)x+(2-5a)≥0;
根據y1、y2的圖象知:a>0,
∴y最小=![]() ≥0
≥0
∴(4a-2)2-4a(2-5a)≤0, ∴(3a-1)2≤0,
而(3a-1)2≥0,只有3a-1=0,解得a= ![]() ,
,
∴拋物線的解析式為:![]()


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:初中數學 來源: 題型:
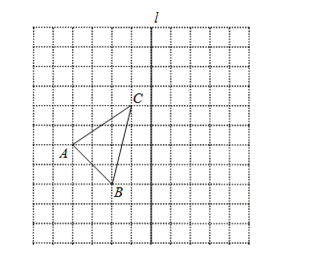
【題目】如圖,在![]() 的正方形網格中,每個小正方形的邊長都為1,網格中有一個格點
的正方形網格中,每個小正方形的邊長都為1,網格中有一個格點![]() (即三角形的頂點都在格點上).
(即三角形的頂點都在格點上).
(1)在圖中作出![]() 關于直線l對稱的
關于直線l對稱的![]() ;(要求A與
;(要求A與![]() ,B與
,B與![]() ,C與
,C與![]() 相對應)
相對應)
(2)作出![]() 繞點C順時針方向旋轉90°后得到的
繞點C順時針方向旋轉90°后得到的![]() ;
;
(3)在(2)的條件下求出線段CB在旋轉中所掃過的面積.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣2ax﹣2的圖象(記為拋物線C1)頂點為M,直線l:y=2x﹣a與x軸,y軸分別交于A,B.
(1)對于拋物線C1,以下結論正確的是 ;
①對稱軸是:直線x=1;②頂點坐標(1,﹣a﹣2);③拋物線一定經過兩個定點.
(2)當a>0時,設△ABM的面積為S,求S與a的函數關系;
(3)將二次函數y=ax2﹣2ax﹣2的圖象C1繞點P(t,﹣2)旋轉180°得到二次函數的圖象(記為拋物線C2),頂點為N.
①當﹣2≤x≤1時,旋轉前后的兩個二次函數y的值都會隨x的增大而減小,求t的取值范圍;
②當a=1時,點Q是拋物線C1上的一點,點Q在拋物線C2上的對應點為Q',試探究四邊形QMQ'N能否為正方形?若能,求出t的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,內角A、B、C的對邊分別為a、b、c.若b2+c2=2b+4c﹣5且a2=b2+c2﹣bc,則△ABC的面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c(a≠0)與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,點A的坐標為(﹣1,0),且OC=OB,tan∠OAC=4.
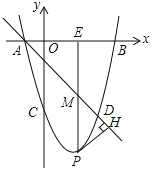
(1)求拋物線的解析式:
(2)若點D和點C關于拋物線的對稱軸對稱,直線AD下方的拋物線上有一點P,過點P作PH⊥AD于點H,作PM平行于y軸交直線AD于點M,交x軸于點E,求△PHM的周長的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
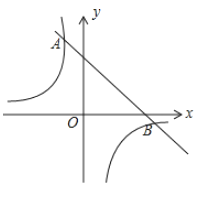
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象相交于
的圖象相交于![]() ,
,![]() 兩點,其中點
兩點,其中點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
(1)根據函數圖象,直接寫出滿足![]() 的
的![]() 的取值范圍是_______;
的取值范圍是_______;
(2)求這兩個函數的表達式;
(3)點![]() 在線段
在線段![]() 上,且
上,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將Rt△ABC繞直角頂點B逆時針旋轉90°得到△DBE,DE的延長線恰好經過AC的中點F,連接AD,CE.
(1)求證:AE=CE;
(2)若BC=![]() ,求AB的長.
,求AB的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
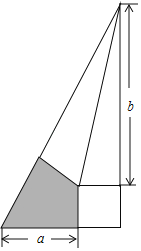
【題目】我國魏晉時期的數學家劉徽將勾股形(古人稱直角三角形為勾股形)分割成一個正方形和兩對全等的直角三角形,得到一個恒等式,后人借助這種分割方法所得的圖形證明了勾股定理.如圖所示,若a=2,b=3,現隨機向該圖形內擲一枚小針,則針尖落在陰影域內的概率為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校3月份開展網絡授課教學,該校隨機抽取部分學生,按四個類別(A、很喜歡;B、喜歡;C、一般;D、不喜歡;)統計它們對網絡授課的接受情況,并將結果繪制成如下兩幅不完整的統計圖:
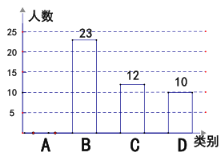
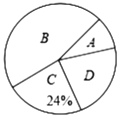
(1)這次共抽取_________名學生進行統計調查;扇形統計圖中,D類所對應的扇形圓心角的大小為_______;
(2)將條形圖補充完整;
(3)該校共有1500名學生,估計該校表示“喜歡”網絡授課的B類的學生大約有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com