
| 1 |
| 2 |
| 3 |
| 2 |

| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
 (2)易知:A點坐標為(-1,0),B點坐標為(4,0),C點坐標為(0,-2),
(2)易知:A點坐標為(-1,0),B點坐標為(4,0),C點坐標為(0,-2),| 5 |
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |


科目:初中數學 來源:不詳 題型:解答題
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| 3 |
| 8 |
 份x(月)滿足的函數關系如圖所示.
份x(月)滿足的函數關系如圖所示.查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| ∫ | ba |
| ∫ | 21 |
| ∫ | 21 |
| 2 |
| x |
| ∫ | 21 |
| ∫ | 21 |
| 3 |
| 2 |
| 7 |
| 2 |
| A.A | B.B | C.C | D.無法比較 |

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| 7 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| 3 |
| 5 |
 且與OE平行,現正方形以每秒
且與OE平行,現正方形以每秒| a |
| 10 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
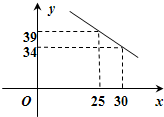 4萬元,且所有資金全部用于生產這三種型號的汽車,三種型號的汽車生產成本和售價如下表:
4萬元,且所有資金全部用于生產這三種型號的汽車,三種型號的汽車生產成本和售價如下表:| A | B | C | |
| 成本(萬元/輛) | 12 | 15 | 18 |
| 售價(萬元/輛) | 14 | 18 | 22 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com