
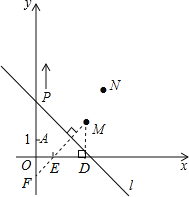
【題目】如圖,A(0,1),M(3,2),N(4,4).動點P從點A出發,沿y軸以每秒1個單位長的速度向上移動,且過點P的直線l:y=﹣x+b也隨之移動,設移動時間為t秒.

(1)當t=3時,求l的解析式;
(2)若點M,N位于l的異側,確定t的取值范圍;
(3)直接寫出t為何值時,點M關于l的對稱點落在坐標軸上.
【答案】(1)y=﹣x+4.(2)若點M,N位于l的異側,t的取值范圍是:4<t<7.(3)當t=1時,落在y軸上,當t=2時,落在x軸上.
【解析】
試題分析:(1)利用一次函數圖象上點的坐標特征,求出一次函數的解析式;
(2)分別求出直線l經過點M、點N時的t值,即可得到t的取值范圍;
(3)找出點M關于直線l在坐標軸上的對稱點E、F,如解答圖所示.求出點E、F的坐標,然后分別求出ME、MF中點坐標,最后分別求出時間t的值.
解:(1)直線y=﹣x+b交y軸于點P(0,b),
由題意,得b>0,t≥0,b=1+t.
當t=3時,b=4,
故y=﹣x+4.
(2)當直線y=﹣x+b過點M(3,2)時,
2=﹣3+b,
解得:b=5,
5=1+t,
解得t=4.
當直線y=﹣x+b過點N(4,4)時,
4=﹣4+b,
解得:b=8,
8=1+t,
解得t=7.
故若點M,N位于l的異側,t的取值范圍是:4<t<7.
(3)如右圖,過點M作MF⊥直線l,交y軸于點F,交x軸于點E,則點E、F為點M在坐標軸上的對稱點.
過點M作MD⊥x軸于點D,則OD=3,MD=2.
已知∠MED=∠OEF=45°,則△MDE與△OEF均為等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,﹣1).
∵M(3,2),F(0,﹣1),
∴線段MF中點坐標為(![]() ,
,![]() ).
).
直線y=﹣x+b過點(![]() ,
,![]() ),則
),則![]() =﹣
=﹣![]() +b,解得:b=2,
+b,解得:b=2,
2=1+t,
解得t=1.
∵M(3,2),E(1,0),
∴線段ME中點坐標為(2,1).
直線y=﹣x+b過點(2,1),則1=﹣2+b,解得:b=3,
3=1+t,
解得t=2.
故點M關于l的對稱點,當t=1時,落在y軸上,當t=2時,落在x軸上.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】已知,如圖,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理過程,請你填空).

解:∵∠BAE+∠AED=180°(已知)
∴ AB ∥ ( )
∴∠BAE= ( 兩直線平行,內錯角相等 )
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣∠2即∠MAE=
∴ ∥NE( )
∴∠M=∠N( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】說明命題“如果a,b,c是△ABC的三邊,那么長為a-1,b-1,c-1的三條線段能構成三角形”是假命題的反例可以是( )
A. a=2,b=2,c=3 B. a=2,b=2,c=2
C. a=3,b=3,c=4 D. a=3,b=4,c=5
查看答案和解析>>
科目:初中數學 來源: 題型:
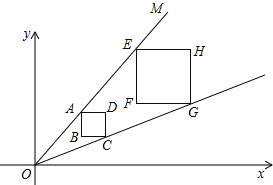
【題目】已知在平面直角坐標系中,點O為坐標原點,過O的直線OM經過點A(6,6),過A作正方形ABCD,在直線OA上有一點E,過E作正方形EFGH,已知直線OC經過點G,且正方形ABCD的邊長為2,正方形EFGH的邊長為3,則點F的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點O是邊AC上一個動點,過O作直線MN∥BC.設MN交∠ACB的平分線于點E,交∠ACB的外角平分線于點F.
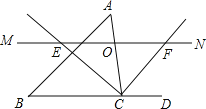
(1)求證:OE=OF;
(2)若CE=12,CF=5,求OC的長;
(3)當點O在邊AC上運動到什么位置時,四邊形AECF是矩形?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班10名學生校服尺寸與對應人數如下表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
學生人數(人) | 1 | 3 | 2 | 2 | 2 |
則這10名學生校服尺寸的中位數為cm.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com