【題目】已知:x=2
+1,y=-1，
求:（1）
的立方根；（2）
的平方根；（3）
的值
【答案】（1）立方根為3；（2）平方根為±3
；（3）7．
【解析】
（1）根據完全平方公式得到x2+2xy+y2=（x+y）2，再代入計算，進一步根據立方根的定義求解即可；
（2）先代入求出x2+y2-2
+1的值，進一步求得平方根；
（3）將x=2+1，y=-1代入（4+2）y2+（2-1）x-8，再根據完全平方公式和平方差公式求值即可．
解：（1）∵x=2+1，y=-1，
∴x2+2xy+y2
=（x+y）2
=（2+1+-1）2
=27，
27的立方根為3；
（2）∵x=2+1，y=-1，
∴x2+y2-2+1
=（2+1）2+（-1）2-2+1
=13+4+4-2-2+1
=18，
18的平方根為±3 ；
（3）∵x=2+1，y=-1，
∴（4+2）y2+（2-1）x-8
=（4+2）（-1）2+（2-1）（2+1）-8
=（4+2）（4-2）+12-1-8
=16-12+12-1-8
=7．
故答案為：（1）立方根為3；（2）平方根為±3 ；（3）7．
期末100分闖關海淀考王系列答案
小學能力測試卷系列答案科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB=90°，AC=30cm，BC=40cm．點P從點A出發，以5cm/s的速度沿AC向終點C勻速移動．過點P作PQ⊥AB，垂足為點Q，以PQ為邊作正方形PQMN，點M在AB邊上，連接CN．設點P移動的時間為t（s）．
（1）PQ=______；（用含t的代數式表示）
（2）當點N分別滿足下列條件時，求出相應的t的值；①點C，N，M在同一條直線上；②點N落在BC邊上；
（3）當△PCN為等腰三角形時，求t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若將代數式中的任意兩個字母交換，代數式不變，則稱這個代數式為完全對稱式，如
就是完全對稱式(代數式中
換成b，b換成，代數式保持不變).下列三個代數式：①
；②
；③
．其中是完全對稱式的是（ ）
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目：初中數學 來源： 題型：
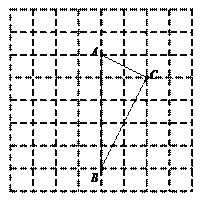
【題目】如圖，在由邊長為1的小正方形組成的網格圖中，有一個格點三角形ABC．（注：頂點均在網格線交點處的三角形稱為格點三角形．）
（1）△ABC是 三角形（填“銳角”、“直角”或“鈍角”）；
（2）若P、Q分別為線段AB、BC上的動點，當PC＋PQ取得最小值時，
① 在網格中用無刻度的直尺，畫出線段PC、PQ．（請保留作圖痕跡．）
② 直接寫出PC＋PQ的最小值： .
查看答案和解析>>
科目：初中數學 來源： 題型：
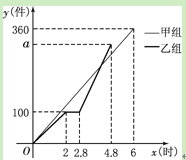
【題目】甲、乙兩組工人同時加工某種零件，乙組工作中有一次停產更換設備，更換設備
后，乙組的工作效率是原來的2倍．兩組各自加工零件的數量
(件)與時間
(時)的函數圖
象如圖所示．
（1）求甲組加工零件的數量y與時間
之間的函數關系式．（2分）
（2）求乙組加工零件總量
的值．（3分）
（3）甲、乙兩組加工出的零件合在一起裝箱，每夠300件裝一箱，零件裝箱的時間忽略不計，求經過多長時間恰好裝滿第1箱？再經過多長時間恰好裝滿第2箱？（5分）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點E是正方形ABCD的對角線BD上一點，并且AD=DE，過點E作EF⊥BD交AB于點F.
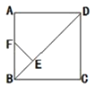
（1）求證：AF=BE,（2）若正方形的邊長為1，求BF的長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】直線y＝kx+k﹣2經過點（m，n+1）和（m+1，2n+3），且﹣2＜k＜0，則n的取值范圍是（ ）
A. ﹣2＜n＜0B. ﹣4＜n＜﹣2C. ﹣4＜n＜0D. 0＜n＜﹣2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點E，F在矩形的邊AD，BC上，點B與點D關于直線EF對稱．設點A關于直線EF的對稱點為G．
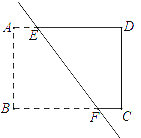
（1）畫出四邊形ABFE關于直線EF對稱的圖形；
（2）若∠FDC＝16°，直接寫出∠GEF的度數為 ；
（3）若BC＝4，CD＝3，寫出求線段EF長的思路．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列敘述中，①所有的正數都是整數；②|a|一定是正數；③無限小數一定是無理數；④(－2)3沒有平方根；⑤
的平方根是±2．其中不正確的個數有（ ）
A.2個B.3個C.4個D.5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com