

 解:(1)∵Rt△AOB在平面直角坐標系中,∠AOB=90°,∠BAO=30°,且A的坐標為(3,0),
解:(1)∵Rt△AOB在平面直角坐標系中,∠AOB=90°,∠BAO=30°,且A的坐標為(3,0),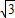 ),
),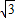 )代入得,
)代入得,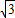 =a×1×(-3),解得a=-
=a×1×(-3),解得a=-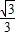 ,
, (x+1)(x-3),即y=-
(x+1)(x-3),即y=-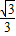 x2+
x2+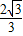 x+
x+ ;
;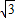 ),⊙C的圓心為點C(-1,0),半徑為1,
),⊙C的圓心為點C(-1,0),半徑為1,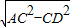 =
= =
=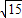 ,
, =
= ,
,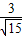 =
=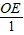 ,解得OE=
,解得OE=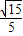 ,
, +
+ ,
, BE•OA=
BE•OA= ×(
×( +
+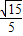 )×3=
)×3=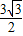 +
+ .
.

 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
 如圖,已知Rt△ABC外切于⊙O,E、F、H為切點,∠ABC=90°,直線FE、CB相交于D點,連接AO、HE、HF,則下列結論:①∠EFH=45°;②∠FEH=45°+∠FAO;③BD=AF;④DH2=AO•DF.其中正確結論的個數為( )
如圖,已知Rt△ABC外切于⊙O,E、F、H為切點,∠ABC=90°,直線FE、CB相交于D點,連接AO、HE、HF,則下列結論:①∠EFH=45°;②∠FEH=45°+∠FAO;③BD=AF;④DH2=AO•DF.其中正確結論的個數為( )| A、1個 | B、2個 | C、3個 | D、4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:
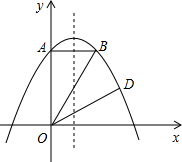 梯形?若存在,請求出所有符合條件的點P的坐標;若不存在,請說明理由.
梯形?若存在,請求出所有符合條件的點P的坐標;若不存在,請說明理由.| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 梯形?若存在,請求出所有符合條件的點P的坐標;若不存在,請說明理由.
梯形?若存在,請求出所有符合條件的點P的坐標;若不存在,請說明理由. ,
, ).
).查看答案和解析>>
科目:初中數學 來源:2011年遼寧省遼陽市中考數學試卷(解析版) 題型:解答題
 ,
, ).
).
查看答案和解析>>
科目:初中數學 來源:2009年湖北省武漢市新洲區初中畢業年級數學試卷(解析版) 題型:選擇題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com