

| 解:(1)C(0,2) , D(1,2); | |
| (2)由y=-2x+4求得B(0,4),A(0,2), 如圖①,折疊后點(diǎn)B與點(diǎn)A重合, 則△ACD≌△BCD,BD=DA, 由(1)得D的坐標(biāo)為(1,2), 設(shè)點(diǎn)C的坐標(biāo)為(0,m)(m>0), 則BC=OB-OC=4-m, 于是AC=BC=4-m, 在Rt△AOC中,由勾股定理,得AC2=OC2+OA2, 即(4-m)2=m2+22, 解得 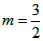 , ,∴點(diǎn)C的坐標(biāo)為 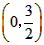 ,D的坐標(biāo)為(1,2); ,D的坐標(biāo)為(1,2); |
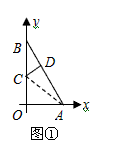 |
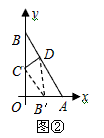
| (3)如圖②,折疊后點(diǎn)B落在OA邊上的點(diǎn)為B', 且B'D∥OB, 則△B'CD≌△BCD,∠OCB'=∠CB'D, 又∵∠CBD=∠CB'D, ∴∠OCB'=∠CBD, 有CB'∥BA, ∴Rt△COB'∽R(shí)t△BOA, 有 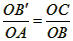 , ,得OC=2OB', 在Rt△B'OC中, 設(shè)OB'=x0(x>0),則OC=2x0, 則B'C=BC=OB-OC=4-2x0, 在Rt△B'OC中,由勾股定理,得B'C2=OC2+OB'2, ∴(4-2x0)2=(2x0)2+x02, 得x20+16x0-16=0, 解得 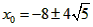 , ,∵x0>0, ∴ 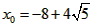 , ,∴點(diǎn)C的坐標(biāo)為 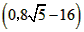 , ,∵B'D∥OB, 則可得點(diǎn)D的橫坐標(biāo)為 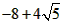 , ,設(shè)點(diǎn)D的縱坐標(biāo)為n, ∵點(diǎn)D在直線y=-2x+4上, ∴ 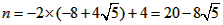 , ,∴點(diǎn)D的坐標(biāo)為 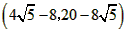 。 。 |
 |



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 的動(dòng)點(diǎn),折疊直角三角形紙片OAB,使折疊后點(diǎn)B與點(diǎn)B'重合,折痕與邊OB交于點(diǎn)C,與邊AB交于點(diǎn)D.
的動(dòng)點(diǎn),折疊直角三角形紙片OAB,使折疊后點(diǎn)B與點(diǎn)B'重合,折痕與邊OB交于點(diǎn)C,與邊AB交于點(diǎn)D.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:新海實(shí)驗(yàn)中學(xué)2008年中考第一次模擬考試數(shù)學(xué)試題 題型:013
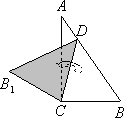
如圖,將一個(gè)直角三角形紙片(∠ACB=90°),沿線段CD折疊,使點(diǎn)B落在點(diǎn)B1處,若∠ACB1=70°,則∠ACD的度數(shù)為
A.10°
B.15°
C.20°
D.25°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
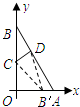 的動(dòng)點(diǎn),折疊直角三角形紙片OAB,使折疊后點(diǎn)B與點(diǎn)B'重合,折痕與邊OB交于點(diǎn)C,與邊AB交于點(diǎn)D.
的動(dòng)點(diǎn),折疊直角三角形紙片OAB,使折疊后點(diǎn)B與點(diǎn)B'重合,折痕與邊OB交于點(diǎn)C,與邊AB交于點(diǎn)D.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2011年《海峽教育報(bào)》初中數(shù)學(xué)綜合練習(xí)(二)(解析版) 題型:解答題
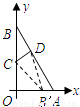
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com