
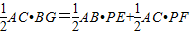
 AB×PE=
AB×PE= AC×BG+
AC×BG+ AC×PF,即可推出答案;
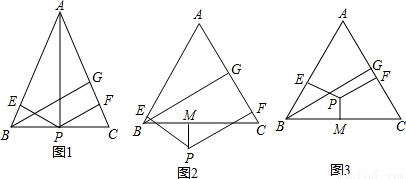
AC×PF,即可推出答案; AC×BG=
AC×BG= AB×PE+
AB×PE+ AC×PF-
AC×PF- BC×PM,即可推出答案;②連接PA、PB、PC,與①類似根據三角形的面積公式能推出BG+PM=PE+PF,即可求出答案.
BC×PM,即可推出答案;②連接PA、PB、PC,與①類似根據三角形的面積公式能推出BG+PM=PE+PF,即可求出答案.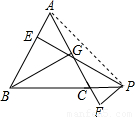
 AB×PE=
AB×PE= AC×BG+
AC×BG+ AC×PF,
AC×PF,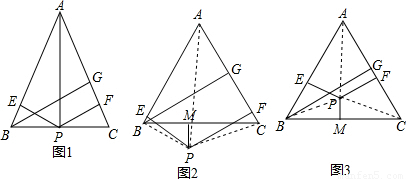
 AC×BG=
AC×BG= AB×PE+
AB×PE+ AC×PF-
AC×PF- BC×PM,
BC×PM, AC×BG+
AC×BG+ BC×PM=
BC×PM= AB×PE+
AB×PE+ AC×PF,
AC×PF,

 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:解答題


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com