
【題目】在平面直角坐標系中,拋物線y=![]() 交x軸于點A、B(點A在點B的左側),交y軸于點C.
交x軸于點A、B(點A在點B的左側),交y軸于點C.
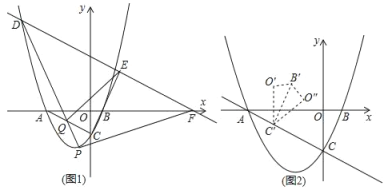
(1)如圖,點D是拋物線在第二象限內的一點,且滿足|xD﹣xA|=2![]() ,過點D作AC的平行線,分別與x軸、射線CB交于點F、E,點P為直線AC下方拋物線上的一動點,連接PD交線段AC于點Q,當四邊形PQEF的面積最大時,在y軸上找一點M,x軸上找一點N,使得PM+MN﹣
,過點D作AC的平行線,分別與x軸、射線CB交于點F、E,點P為直線AC下方拋物線上的一動點,連接PD交線段AC于點Q,當四邊形PQEF的面積最大時,在y軸上找一點M,x軸上找一點N,使得PM+MN﹣![]() NB取得最小值,求這個最小值;
NB取得最小值,求這個最小值;
(2)如圖2,將△BOC沿著直線AC平移得到△B′O′C′,再將△B'O′C′沿B′C′翻折得到△B′O″C′,連接BC′、O″B,則△C′BO″能否構成等腰三角形?若能,請直接寫出所有符合條件的點O″的坐標,若不能,請說明理由.
【答案】(1)P′W=3![]() ;(2)點O″的坐標為(﹣
;(2)點O″的坐標為(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
1)根據|xD﹣xA|=2![]() ,求出點D的坐標,轉換四邊形PQEF的面積最大即為線段PH最大,PM+MN﹣
,求出點D的坐標,轉換四邊形PQEF的面積最大即為線段PH最大,PM+MN﹣![]() NB取得最小值,將這三條線段轉化為共線即可.
NB取得最小值,將這三條線段轉化為共線即可.
(2)設點O′、B′、C′的坐標,求出點O″的坐標,利用兩點間距離公式表示線段長度,分三種情況討論即可.
(1)令![]() =0,
=0,
解得x1=![]() ,x2=﹣4
,x2=﹣4![]() ,
,
∴A(﹣4![]() ,0),B(
,0),B(![]() ,0),
,0),
令x=0,y=﹣2![]() ,
,
∴C(0,﹣2![]() ),
),
∵|xD﹣xA|=2![]() ,點D是拋物線在第二象限內的一點,
,點D是拋物線在第二象限內的一點,
∴D的橫坐標為﹣6![]() ,
,
∴D(﹣6![]() ,7
,7![]() ),
),
設直線BC的解析式為y=kx+b,
則有![]()
解得![]()
∴直線BC的解析式為y=2x﹣2![]() ,
,
設直線AC的解析式為y=k1x+b1,
則有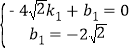
解得
∴直線AC的解析式為y=﹣![]() x﹣2
x﹣2![]() ,
,
∵DE∥AC,
∴設直線DE的解析式為y=﹣![]() x+b2,代入點D(﹣6
x+b2,代入點D(﹣6![]() ,7
,7![]() ),
),
解得b2=4![]() ,
,
∴直線DE的解析式為y=﹣![]() x+4
x+4![]() ,
,
令y=0,此時x=8![]() ,
,
∴F(8![]() ,0),
,0),
令2x﹣2![]() =﹣
=﹣![]() x+4
x+4![]() ,
,
解得x=![]() ,
,
∴E(![]() ,
,![]() ),
),
∵S四邊形PQEF=S△PDF﹣S△PQE=S△PDF﹣S△DAE,
∵D、A、E是固定點,
∴S△DAE是固定值,即要使四邊形PQEF的面積最大,只需△PDF的面積最大,
如圖1所示,
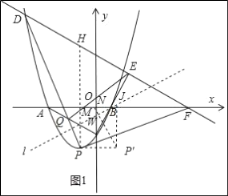
過點P作x軸的垂線交DF于點H,則S△PDF=![]() PH|xF﹣xD|=7
PH|xF﹣xD|=7![]() PH,
PH,
∴當PH最大時,S△PDF最大,
設點P的坐標為(a,![]() a2+
a2+![]() a﹣2
a﹣2![]() ),則點H為(a,﹣
),則點H為(a,﹣![]() a+4
a+4![]() ),
),
∴PH=﹣![]() a2﹣2a+6
a2﹣2a+6![]() =﹣
=﹣![]() (a+2
(a+2![]() )2+8
)2+8![]() ,
,
∴當a=﹣2![]() 時,PH最大,
時,PH最大,
此時P(﹣2![]() ,﹣3
,﹣3![]() ),
),
作點P關于y軸的對稱點P′(2![]() ,﹣3
,﹣3![]() ),
),
過點B作直線l:y=![]() x﹣
x﹣![]() ,
,
過點P′作直線l的垂線交l于點W,交y軸于點M,交x軸于點N,
∴![]() NB=NW,
NB=NW,
∴PM+MN﹣![]() NB=PM+MN﹣NW=P′N﹣NW=P′W,
NB=PM+MN﹣NW=P′N﹣NW=P′W,
∴P′W即為所求,
過P′作y軸的平行線交l于點J,
則J(2![]() ,
,![]() ),
),
則JP′=![]() ,
,
則P′W=![]() JP′=3
JP′=3![]() .
.
(2)設△BOC在水平方向上移動了2![]() t個單位,則在豎直方向上移動了
t個單位,則在豎直方向上移動了![]() t個單位,
t個單位,
則C′(﹣2![]() t,﹣2
t,﹣2![]() t+
t+![]() t),O′(﹣2
t),O′(﹣2![]() t,
t,![]() t),
t),
如圖2所示,過O″作y軸的平行線交O′B′的延長線于點M,
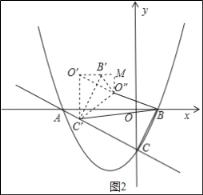
O′O″=2×![]() ×
×![]() =
=![]() ,
,
∴O″M=![]() ,O′M=
,O′M=![]() ,
,
∴O″(![]() ﹣2
﹣2![]() t,﹣
t,﹣![]() +
+![]() t),
t),
∴C′B=![]() =
=![]() ,
,
C′O″=2![]() ,
,
O″B=![]() =
=![]()
①![]() =2
=2![]() ,無解.
,無解.
②![]() =
=![]() ,解得t=-1,
,解得t=-1,
∴O″(﹣![]() ,
,![]() ),
),
③![]() =2
=2![]() ,解得t1=
,解得t1=![]() ,t2=
,t2=![]() ,
,
∴O″(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
綜上所述:點O″的坐標為(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
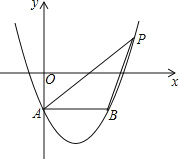
【題目】如圖,在平面直角坐標系中,拋物線y=x2-2x-1交y軸于點A,過點A作AB∥x軸交拋物線于點B,點P在拋物線上,連結PA、PB,若點P關于x軸的對稱點恰好落在直線AB上,則△ABP的面積是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在趣味運動會“定點投籃”項目中,我校七年級八個班的投籃成績![]() 單位:個
單位:個![]() 分別為:24,20,19,20,22,23,20,
分別為:24,20,19,20,22,23,20,![]() 則這組數據中的眾數和中位數分別是
則這組數據中的眾數和中位數分別是![]()
![]()
A. 22個、20個 B. 22個、21個 C. 20個、21個 D. 20個、22個
查看答案和解析>>
科目:初中數學 來源: 題型:
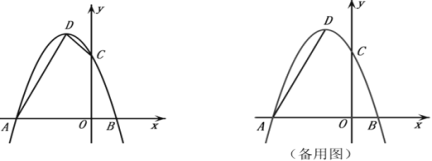
【題目】已知拋物線![]() 過點
過點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,![]() ,交y軸于點
,交y軸于點![]() ,頂點為
,頂點為![]() .
.
(1)求拋物線解析式;
(2)在第一象限內的拋物線上求點![]() ,使
,使![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)![]() 是第一象限內拋物線上一點,
是第一象限內拋物線上一點,![]() 是線段
是線段![]() 上一點,點
上一點,點![]() 在
在![]() 點右側,且滿足
點右側,且滿足![]() ,當
,當![]() 為何值時,滿足條件的點
為何值時,滿足條件的點![]() 只有一個?
只有一個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等腰三角形,AB=AC,點D是AB上一點,過點D作DE⊥BC交BC于點E,交CA延長線于點F.
(1)證明:△ADF是等腰三角形;
(2)若∠B=60°,BD=4,AD=2,求EC的長,

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只不透明袋子中裝有三只大小、質地都相同的小球,球面上分別標有數字1、﹣2、3,攪勻后先從中任意摸出一個小球(不放回),記下數字作為點A的橫坐標,再從余下的兩個小球中任意摸出一個小球,記下數字作為點A的縱坐標.
(1)用畫樹狀圖或列表等方法列出所有可能出現的結果;
(2)求點A落在第四象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,點P(x0,y0)到直線Ax+By+C=0(A2+B2≠0)的距離公式為:d=![]() ,
,
例如,求點P(1,3)到直線4x+3y﹣3=0的距離.
解:由直線4x+3y﹣3=0知:A=4,B=3,C=﹣3
所以P(1,3)到直線4x+3y﹣3=0的距離為:d=![]() =2
=2
根據以上材料,解決下列問題:
(1)求點P1(1,-1)到直線3x﹣4y﹣5=0的距離.
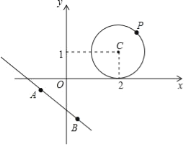
(2)已知:⊙C是以點C(2,1)為圓心,1為半徑的圓,⊙C與直線y=﹣![]() x+b相切,求實數b的值;
x+b相切,求實數b的值;
(3)如圖,設點P為問題2中⊙C上的任意一點,點A,B為直線3x+4y+5=0上的兩點,且AB=2,請求出△ABP面積的最大值和最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展“走進中國數學史”為主題的知識競賽活動,八、九年級各有200名學生參加競賽,為了解這兩個年級參加競賽學生的成績情況,從中各隨機抽取20名學生的成績,數據如下:
八年級 | 91 | 89 | 77 | 86 | 71 | 九年級 | 84 | 93 | 66 | 69 | 76 |
51 | 97 | 93 | 72 | 91 | 87 | 77 | 82 | 85 | 88 | ||
81 | 92 | 85 | 85 | 95 | 90 | 88 | 67 | 88 | 91 | ||
88 | 88 | 90 | 64 | 91 | 96 | 68 | 97 | 99 | 88 |
整理上面數據,得到如下統計表:
成績 人數 年級 |
|
|
|
|
|
八年級 | 1 | 1 | 3 | 7 | 8 |
九年級 | 0 | 4 | 2 | 8 | 6 |
樣本數據的平均數、中位數、眾數、方差如下表所示:
統計表 年級 | 平均數 | 中位數 | 眾數 | 方差 |
八年級 | 83.85 | 88 | 91 | 127.03 |
九年級 | 83.95 | 87.5 | | 99.45 |
根據以上信息,回答下列問題:
(1)寫出上表中眾數![]() 的值.
的值.
(2)試估計八、九年級這次選拔成績80分以上的人數和.
(3)你認為哪個年級學生的競賽成績較好?說明你的理由.(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
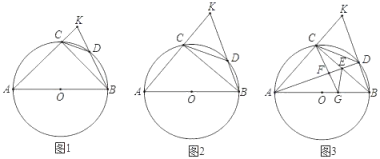
【題目】已知AB是⊙O的直徑,點C是弧AB的中點,點D在弧BC上,BD、AC的延長線交于點K,連接CD.
(1)求證:∠AKB﹣∠BCD=45°;
(2)如圖2,若DC=![]() DB時,求證:BC=2CK;
DB時,求證:BC=2CK;
(3)在(2)的條件下,連接BC交AD于點E,過點C作CF⊥AD于點F,延長CF交AB于點G,連接GE,若GE=5,求CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com