
【題目】已知:如圖所示,O為數軸的原點,A,B分別為數軸上的兩點,A點對應的數為﹣30,B點對應的數為100.
(1)A、B的中點C對應的數是 ;
(2)若點D數軸上A、B之間的點,D到B的距離是D到A的距離的3倍,求D對應的數.(提示:數軸上右邊的點對應的數減去左邊對應的數等于這兩點間的距離);
(3)若P點和Q點是數軸上的兩個動點,當P點從B點出發,以6個單位長度/秒的速度向左運動時,Q點也從A點出發,以4個單位長度/秒的速度向右運動,設兩點在數軸上的E點處相遇,那么E點對應的數是多少?
![]()
【答案】(1)35;(2)點D對應的數是2.5;(3)E點對應的數是22.
【解析】
(1)先計算線段AB的長,再確定中點C,根據數軸得到點C表示的數是多少;
(2)設點D對應的數是x,根據線段DB、DA間關系,得方程求解即可;
(3)根據:點P運動的距離+點Q運算的距離=AB,先求出相遇時間,再求相遇點E表示的數是多少.
解:(1)點A表示的數是﹣30,點B表示的數是100,
所以AB=100﹣(﹣30)=130
因為點C是AB的中點,
∴AC=BC=![]() =65
=65
A、B的中點C對應的數是100﹣65=35.
故答案為:35.
(2)設點D對應的數是x,則由題意,
得100﹣x=3[x﹣(﹣30)]
解得,x=2.5
所以點D對應的數是2.5.
(3)設t秒后相遇,
由題意,4t+6t=130,
解得,t=13,
BE=100﹣6t=78,
100﹣78=22
答:E點對應的數是22.
故答案為:(1)35;(2)點D對應的數是2.5;(3)E點對應的數是22.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系中,△ABC的頂點都在網格點上,其中C點坐標為(1,2),

(1)請畫出△ABC向左平移1個單位長度,再向上平移2個單位長度后的△A′B′C′,(其中A′、B′、C′分別是A、B、C的對應點)
(2)直接寫出A′、B′、C′三點的坐標:A′(_____,______);B′(_____,______);C′(_____,______).
(3)△ABC的面積為______________平方單位
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為提倡節約用水,準備實行自來水“階梯計費”方式,用戶用水不超出基本用水量的部分享受基本價格,超出基本用水量的部分實行加價收費,為更好地做決策,自來水公司隨機抽取部分用戶的用水量數據,并繪制了如圖不完整的統計圖(每組數據包括右端點但不包括左端點),請你根據統計圖解決下列問題:
(1)此次抽樣調查的樣本容量是 .
(2)補全頻數分布直方圖.
(3)如果自來水公司將基本用水量定為每戶25噸,那么該地區6萬用戶中約有多少用戶的用水全部享受基本價格?
查看答案和解析>>
科目:初中數學 來源: 題型:
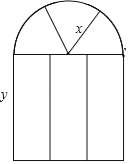
【題目】某窗戶的形狀如圖所示(圖中長度單位:cm),其中上部是半徑為xcm的半圓形,下部是寬為ycm的長方形.
(1)用含x,y的式子表示窗戶的面積S;
(2)當x=40,y=120時,求窗戶的面積S.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜邊AB上一動點(不與點A、B重合),PQ⊥AB交△ABC的直角邊于點Q,設AP為x,△APQ的面積為y,則下列圖象中,能表示y關于x的函數關系的圖象大致是( )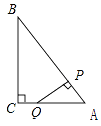
A.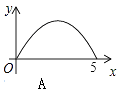
B.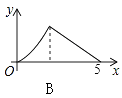
C.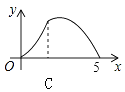
D.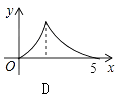
查看答案和解析>>
科目:初中數學 來源: 題型:
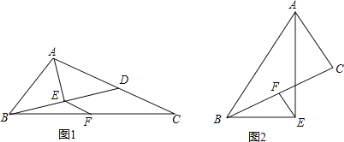
【題目】如圖,在△ABC中,AE平分∠BAC,BE⊥AE于點E,點F是BC的中點.
(1)如圖1,BE的延長線與AC邊相交于點D,求證:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如圖2,請直接寫出線段AB、AC、EF之間的數量關系。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,ABCD 中,∠ABC、∠ADC的平分線分別交AD、BC于點E、F.
(1)求證:四邊形EBFD是平行四邊形;
(2)小明在完成(1)的證明后繼續進行了探索.連接AF、CE,分別交BE、FD于點G、H,得到四邊形EGFH.此時,他猜想四邊形EGFH是平行四邊形,請在框圖(圖2)中補全他的證明思路.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCF中,∠ACB=90°,點E是AB邊的中點,點F恰是點E關于AC所在直線的對稱點.
(1)證明:四邊形CFAE為菱形;
(2)連接EF交AC于點O,若BC=10,求線段OF的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com