A
本題考查多邊形的內角和與外角和、方程的思想.關鍵是記住內角和的公式與外角和的特征,還需要懂得挖掘此題隱含著邊數為正整數這個條件.本題既可用整式方程求解,也可用不等式確定范圍后求解.
解法1:設邊數為n,這個外角為x度,則0<x<180°根據題意,得
(n-2)?180°+x=570°
解之,得n=
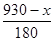
.
∵n為正整數,
∴930-x必為180的倍數,
又∵0<x<180,
∴n=5.
解法2:∵0<x<180.
∴570-180<570-x<570,即390<570-x<570.
又∵(n-2)?180°=570-x,
∴390<(n-2)?180°<570,
解之得4.2<n<5.2.
∵邊數n為正整數,
∴n=5.
故選A.
此題較難,考查比較新穎,涉及到整式方程,不等式的應用.

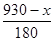 .
.

 全程金卷系列答案
全程金卷系列答案