
【題目】如圖,已知一次函數y1= ![]() x+b的圖象l與二次函數y2=﹣x2+mx+b的圖象C′都經過點B(0,1)和點C,且圖象C′過點A(2﹣
x+b的圖象l與二次函數y2=﹣x2+mx+b的圖象C′都經過點B(0,1)和點C,且圖象C′過點A(2﹣ ![]() ,0).
,0).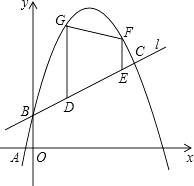
(1)求二次函數的最大值;
(2)設使y2>y1成立的x取值的所有整數和為s,若s是關于x的方程 ![]() =0的根,求a的值;
=0的根,求a的值;
(3)若點F、G在圖象C′上,長度為 ![]() 的線段DE在線段BC上移動,EF與DG始終平行于y軸,當四邊形DEFG的面積最大時,在x軸上求點P,使PD+PE最小,求出點P的坐標.
的線段DE在線段BC上移動,EF與DG始終平行于y軸,當四邊形DEFG的面積最大時,在x軸上求點P,使PD+PE最小,求出點P的坐標.
【答案】
(1)解:∵二次函數y2=﹣x2+mx+b經過點B(0,1)與A(2﹣ ![]() ,0),
,0),
∴ ![]() ,
,
解得 ![]()
∴l:y1= ![]() x+1;
x+1;
C′:y2=﹣x2+4x+1.
∵y2=﹣x2+4x+1=﹣(x﹣2)2+5,
∴ymax=5
(2)解:聯立y1與y2得: ![]() x+1=﹣x2+4x+1,解得x=0或x=
x+1=﹣x2+4x+1,解得x=0或x= ![]() ,
,
當x= ![]() 時,y1=
時,y1= ![]() ×
× ![]() +1=
+1= ![]() ,
,
∴C( ![]() ,
, ![]() ).
).
使y2>y1成立的x的取值范圍為0<x< ![]() ,
,
∴s=1+2+3=6.
代入方程得 ![]()
解得a= ![]() ;
;
經檢驗a= ![]() 是分式方程的解
是分式方程的解
(3)解:∵點D、E在直線l:y1= ![]() x+1上,
x+1上,
∴設D(p, ![]() p+1),E(q,
p+1),E(q, ![]() q+1),其中q>p>0.
q+1),其中q>p>0.
如答圖1,過點E作EH⊥DG于點H,則EH=q﹣p,DH= ![]() (q﹣p).
(q﹣p).

在Rt△DEH中,由勾股定理得:EH2+DH2=DE2,即(q﹣p)2+[ ![]() (q﹣p)]2=(
(q﹣p)]2=( ![]() )2,
)2,
解得q﹣p=2,即q=p+2.
∴EH=2,E(p+2, ![]() p+2).
p+2).
當x=p時,y2=﹣p2+4p+1,
∴G(p,﹣p2+4p+1),
∴DG=(﹣p2+4p+1)﹣( ![]() p+1)=﹣p2+
p+1)=﹣p2+ ![]() p;
p;
當x=p+2時,y2=﹣(p+2)2+4(p+2)+1=﹣p2+5,
∴F(p+2,﹣p2+5),
∴EF=(﹣p2+5)﹣( ![]() p+2)=﹣p2﹣
p+2)=﹣p2﹣ ![]() p+3.
p+3.
S四邊形DEFG= ![]() (DG+EF)EH=
(DG+EF)EH= ![]() [(﹣p2+
[(﹣p2+ ![]() p)+(﹣p2﹣
p)+(﹣p2﹣ ![]() p+3)]×2=﹣2p2+3p+3
p+3)]×2=﹣2p2+3p+3
∴當p= ![]() 時,四邊形DEFG的面積取得最大值,
時,四邊形DEFG的面積取得最大值,
∴D( ![]() ,
, ![]() )、E(
)、E( ![]() ,
, ![]() ).
).
如答圖2所示,過點D關于x軸的對稱點D′,則D′( ![]() ,﹣
,﹣ ![]() );
);
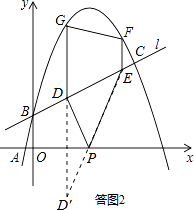
連接D′E,交x軸于點P,PD+PE=PD′+PE=D′E,
由兩點之間線段最短可知,此時PD+PE最小.
設直線D′E的解析式為:y=kx+b,
則有 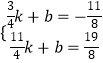 ,
,
解得 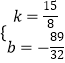
∴直線D′E的解析式為:y= ![]() x﹣
x﹣ ![]() .
.
令y=0,得x= ![]() ,
,
∴P( ![]() ,0).
,0).
【解析】(1)用待定系數法將點B、點A代入一次函數解析式和二次函數解析式,就可以求出兩函數的解析式,再求出二次函數的頂點坐標,即可求出函數的最大值。
(2)先求出拋物線與直線BC的兩交點坐標,觀察圖像,寫出使y2>y1成立的x的取值范圍,求出所有整數的和s的值,再將x=s代入方程,既可求出a的值。注意:此方程式分式方程必須檢驗。
(3)抓住已知條件中的長度為 5 的線段DE在線段BC上移動,EF與DG始終平行于y軸,因此添加輔助線,過點E作EH⊥DG于點H,D、E兩點再直線BC上,設出這兩點的坐標,根據勾股定理,得出EH=2,E(p+2,![]() p+2),再將當x=p時,當x=p+2時,分別代入二次函數解析式,求出對應的函數值,即可表示出點F、點G的坐標,再求出DG、EF的長,根據梯形的面積求出s與t的函數關系式,求出頂點坐標,即可求得p的值,并求出點D、E的坐標,要在x軸上求點P,使PD+PE最小,因此過點D作關于x軸的對稱點D′,,求出直線D′E的解析式,即可求出點P的坐標
p+2),再將當x=p時,當x=p+2時,分別代入二次函數解析式,求出對應的函數值,即可表示出點F、點G的坐標,再求出DG、EF的長,根據梯形的面積求出s與t的函數關系式,求出頂點坐標,即可求得p的值,并求出點D、E的坐標,要在x軸上求點P,使PD+PE最小,因此過點D作關于x軸的對稱點D′,,求出直線D′E的解析式,即可求出點P的坐標
【考點精析】解答此題的關鍵在于理解確定一次函數的表達式的相關知識,掌握確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法,以及對二次函數的最值的理解,了解如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a.


科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE,將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連結AG、CF.下列結論:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
則正確結論的個數有( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c經過A(﹣1,0)、B(3,0)兩點,且與y軸相交于點C,直線l是拋物線的對稱軸.
(1)求拋物線的函數關系式;
(2)設點P是直線l上的一個動點,當點P到點A、點C的距離之和最短時,求點P的坐標;
(3)點M也是直線l上的動點,且△MAC為直角三角形,請直接寫出所有符合條件的點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,三角形紙片ABC中,∠A=65°,∠B=75°,將∠C沿DE對折,使點C落在ΔABC外的點![]() 處,若∠1=20°,則∠2的度數為( )
處,若∠1=20°,則∠2的度數為( )

A. 80°B. 90°
C. 100°D. 110°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名選手在同等條件下進行射擊對抗賽,他們各射靶10次,為了比較兩人的成績,制作了如下統計圖表:
甲、乙射擊成績統計表
平均數 | 眾數 | 中位數 | 方差 | 10環次數 | |
甲 | 8 | ||||
乙 |

(1)請補全上述圖表(請直接在表中填空和補全折線圖);
(2)如果規定成績較穩定者勝出,你認為誰應勝出?說明你的理由;
(3)如果希望(2)中的另一名選手勝出,根據圖表中的信息,應該制定怎樣的評判規則?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)過點C畫AB的平行線CD;
(2)過點C畫AB的垂線,垂足為E;
(3)線段CE的長度是點C到直線__________的距離;
(4)連接CA、CB,在線段CA、CB、CE中,線段__________最短,理由:______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A、D、C、F在同一條直線上,AB=DE,BC=EF,要使△ABC≌△DEF,還需要添加一個條件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子中,共有“一白三黑”四個圍棋子,其除顏色外無其他區別.
(1)隨機地從盒子中取出1子,則提出的是白子的概率是多少?
(2)隨機地從盒子中取出1子,不放回再取出第二子,請用畫樹狀或列表的方式表示出所有可能的結果,并求出恰好取出“一黑一白”的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=x+4與坐標軸分別交于A,B兩點,拋物線y=﹣x2+bx+c過A,B兩點,點D為線段AB上一動點,過點D作CD⊥x軸于點C,交拋物線于點E.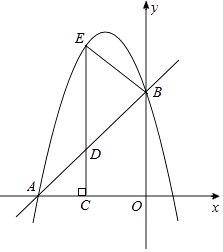
(1)求拋物線的解析式.
(2)求△ABE面積的最大值.
(3)連接BE,是否存在點D,使得△DBE和△DAC相似?若存在,求出點D坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com