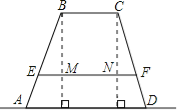
【題目】某高中學校為高一新生設計的學生板凳的正面視圖如圖所示，其中BA=CD，BC=20cm，BC、EF平行于地面AD且到地面AD的距離分別為40cm、8cm．為使板凳兩腿底端A、D之間的距離為50cm，那么橫梁EF應為多長？（材質及其厚度等暫忽略不計）．
科目：初中數學 來源： 題型：
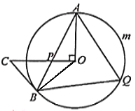
【題目】如圖，AB是⊙O的弦，過點O作OC⊥OA，OC交于AB于P，且CP=CB．
（1）求證：BC是⊙O的切線；
（2）已知∠BAO=25°，點Q是弧AmB上的一點.
①求∠AQB的度數；
②若OA=18，求弧AmB的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（發現）如圖，點E，F分別在正方形ABCD的邊BC，CD上，連接EF．因為AB=AD，所以把ΔABE繞A逆時針旋轉90°至ΔADG，可使AB與AD重合．因為∠CDA=∠B=90°，所以∠FDG=180°，所以F、D、G共線．
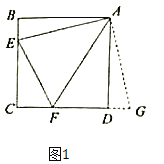
如果__________（填一個條件），可得ΔAEF≌ΔAGF．經過進一步研究我們可以發現：當BE，EF，FD滿足__________時，∠EAF=45°．
（應用）
如圖，在矩形ABCD中，AB=6，AD=m，點E在邊BC上，且BE=2．
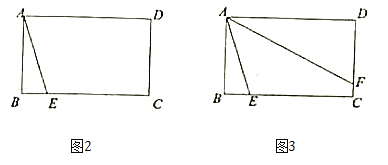
（1）若m=8，點F在邊DC上，且∠EAF=45°（如圖），求DF的長；
（2）若點F在邊DC上，且∠EAF=45°，求m的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC是等腰直角三角形，∠ACB=90°，點E、F分別是邊BC、AC的中點，P是AB上一點，以PF為一直角邊作等腰直角三角形PFQ，且∠FPQ=90°，若AB=10，PB=1，則QE的值為（ ）
A. 3 B. 3
C. 4 D. 4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司推出一款產品，經市場調查發現，該產品的日銷售量y（個）與銷售單價x（元）之間滿足一次函數關系．關于銷售單價，日銷售量，日銷售利潤的幾組對應值如下表：
銷售單價x（元） | 85 | 95 | 105 | 115 |
日銷售量y（個） | 175 | 125 | 75 | m |
日銷售利潤w（元） | 875 | 1875 | 1875 | 875 |
（注：日銷售利潤=日銷售量×（銷售單價﹣成本單價））
（1）求y關于x的函數解析式（不要求寫出x的取值范圍）及m的值；
（2）根據以上信息，填空：
該產品的成本單價是 元，當銷售單價x= 元時，日銷售利潤w最大，最大值是 元；
（3）公司計劃開展科技創新，以降低該產品的成本，預計在今后的銷售中，日銷售量與銷售單價仍存在（1）中的關系．若想實現銷售單價為90元時，日銷售利潤不低于3750元的銷售目標，該產品的成本單價應不超過多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
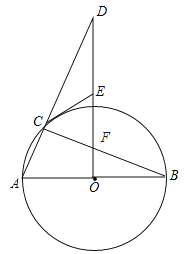
【題目】如圖，
是
直徑，
于點
，連接
交于點
，過點作的切線交
于點
，連
接交于點
（1）求證：
（2）連接
并延長，交于點
，填空：
①當
的度數為_________時，四邊形
為菱形；
②當的度數為__________時，四邊形
為正方形；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某電視臺在它的娛樂性節目中每期抽出兩名場外幸運觀眾，有一期甲、乙兩人被抽為場外幸運觀眾，他們獲得了一次抽獎的機會，在如圖所示的翻獎牌的正面4個數字中任選一個，選中后翻開，可以得到該數字反面的獎品，第一個人選中的數字第二個人不能再選擇了．
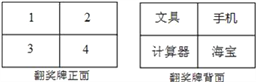
（1）如果甲先抽獎，那么甲獲得“手機”的概率是多少？
（2）小亮同學說：甲先抽獎，乙后抽獎，甲、乙兩人獲得“手機”的概率不同，且甲獲得“手機”的概率更大些．你同意小亮同學的說法嗎？為什么？請用列表或畫樹狀圖分析．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）問題發現
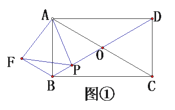
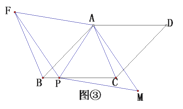
如圖①，矩形
的對角線
交于點
，且
，點
為線段
上任意一點，以
為邊作等邊三角形
，連接
，則與
之間的數量關系是 ；
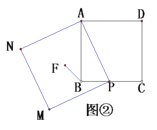
（2）類比延伸
如圖②，在正方形中，點為
邊上任意一點，以為邊作正方形
，
為正方形
的中心，連接，直接寫出與
的數量關系為 ；
（3）拓展遷移
如圖③，在菱形中，
，點
為邊上一點，以為對角線作菱形，滿足
，連接，猜想與的數量關系，并證明你的結論．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
