
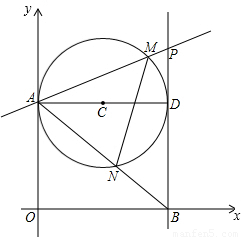
 如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.
如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.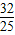 的k值?若存在,請求出符合的k值;若不存在,請說明理由.
的k值?若存在,請求出符合的k值;若不存在,請說明理由.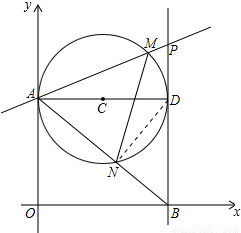 ∵AD是⊙C的直徑,
∵AD是⊙C的直徑,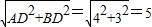 ,
, AB•DN=
AB•DN= AD•DB
AD•DB =
=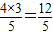 ,
,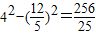 ,
,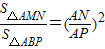 ,即
,即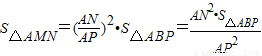 (8分)
(8分) PB•AD=
PB•AD= (4k+3)×4=2(4k+3),
(4k+3)×4=2(4k+3), ,
, ,k2=2-
,k2=2-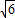 (9分)
(9分) PB•AD=
PB•AD= [-(4k+3)]×4=-2(4k+3)
[-(4k+3)]×4=-2(4k+3)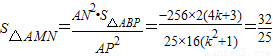
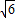 或k=-2時,△AMN的面積等于
或k=-2時,△AMN的面積等于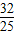 (10分)
(10分)

科目:初中數學 來源: 題型:
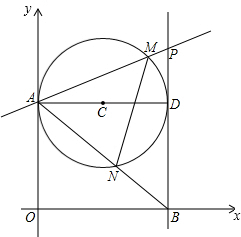 如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.
如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.| 32 | 25 |
查看答案和解析>>
科目:初中數學 來源: 題型:
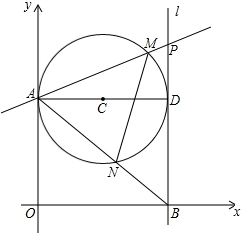 如圖,第一象限內半徑為4的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+6.
如圖,第一象限內半徑為4的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+6.| 128 | 25 |
查看答案和解析>>
科目:初中數學 來源: 題型:
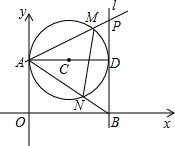 如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.設⊙C與PA交于點M,與AB交于點N,則S△AMN=
如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.設⊙C與PA交于點M,與AB交于點N,則S△AMN=| 32 |
| 25 |
| 6 |
| 6 |
查看答案和解析>>
科目:初中數學 來源:2013年四川省成都市中考數學模擬試卷(二)(解析版) 題型:填空題
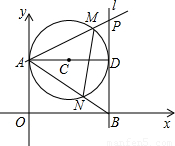 如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.設⊙C與PA交于點M,與AB交于點N,則
如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸于點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3.設⊙C與PA交于點M,與AB交于點N,則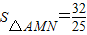 時,k= .
時,k= .查看答案和解析>>
科目:初中數學 來源:2012屆江蘇省蘇州市初三上學期期中考試數學卷 題型:解答題
(本題滿分9分)如圖,第一象限內半徑為2的⊙C與y軸相切于點A,作直徑AD,過點D作⊙C的切線l交x軸子點B,P為直線l上一動點,已知直線PA的解析式為:y=kx+3。
(1)設點P的縱坐標為p,寫出p隨k變化的函數關系式。
(2)設⊙C與PA交于點M,與AB交于點N,則不論動點P處于直線l上(除點B以外)的什么位置時,都有△AMN∽△ABP。請你對于點P處于圖中位置時的兩三角形相似給予證明;
(3)是否存在使△AMN的面積等于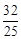 的k值?若存在,請求出符合的k值;若不存在,請說明理由。
的k值?若存在,請求出符合的k值;若不存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com