
【題目】如圖,在平面直角坐標系中,一次函數y=kx+b與反比例函數y=![]() (m≠0)的圖象交于點A(3,1),且過點B(0,﹣2).
(m≠0)的圖象交于點A(3,1),且過點B(0,﹣2).
(1)求反比例函數和一次函數的表達式;
(2)如果點P是x軸上一點,且△ABP的面積是3,求點P的坐標.
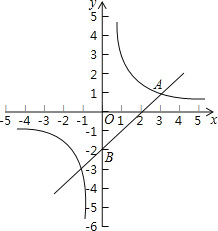
【答案】(1)y=![]() ;y=x-2;(2)(0,0)或(4,0)
;y=x-2;(2)(0,0)或(4,0)
【解析】試題分析:(1)利用待定系數法即可求得函數的解析式;
(2)首先求得AB與x軸的交點,設交點是C,然后根據S△ABP=S△ACP+S△BCP即可列方程求得P的橫坐標.
試題解析:(1)∵反比例函數y=![]() (m≠0)的圖象過點A(3,1),
(m≠0)的圖象過點A(3,1),
∴3=![]()
∴m=3.
∴反比例函數的表達式為y=![]() .
.
∵一次函數y=kx+b的圖象過點A(3,1)和B(0,-2).
∴![]() ,
,
解得: ![]() ,
,
∴一次函數的表達式為y=x-2;
(2)令y=0,∴x-2=0,x=2,
∴一次函數y=x-2的圖象與x軸的交點C的坐標為(2,0).
∵S△ABP=3,
![]() PC×1+
PC×1+![]() PC×2=3.
PC×2=3.
∴PC=2,
∴點P的坐標為(0,0)、(4,0).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知一次函數![]() 與
與![]() (k≠0)的圖象相交于點P(1,-6).
(k≠0)的圖象相交于點P(1,-6).
(1)求一次函數![]() 的解析式;
的解析式;
(2)若點Q(m,n)在函數![]() 的圖象上,求2n-6m+9的值.
的圖象上,求2n-6m+9的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學在創建“特色校園”的活動中,將本校的辦學理念做成宣傳牌AB,放置在教學樓的頂部(如圖所示)。小明在操場上的點D處,用1m高的測角儀CD,從點C測得宣傳牌的底部B的仰角為37,然后向教學樓正方向走了4米到達點F處,又從點E測得宣傳牌頂部A仰角為45.已知教學樓高BM=17米,且點A、B、M在同一直線上,求宣傳牌AB高度(結果精確到0.1米。參考數據:![]() ,sin37≈0.60,cos37≈0.81,tan37≈0.75).
,sin37≈0.60,cos37≈0.81,tan37≈0.75).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊![]() 中,點
中,點![]() 在邊
在邊![]() 上,
上,![]() 過點
過點![]() 且分別與邊
且分別與邊![]() 、
、![]() 相交于點
相交于點![]() 、
、![]() 、
、![]() 是
是![]() 上的點,判斷下列說法錯誤的是( )
上的點,判斷下列說法錯誤的是( )
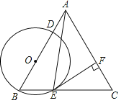
A. 若![]() ,則
,則![]() 是
是![]() 的切線 B. 若
的切線 B. 若![]() 是
是![]() 的切線,則
的切線,則![]()
C. 若![]() ,則
,則![]() 是
是![]() 的切線 D. 若
的切線 D. 若![]() ,則
,則![]() 是
是![]() 的切線
的切線
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:兩邊平方和等于第三邊平方的2倍的三角形叫做奇異三角形.
例如:某三角形三邊長分別是2,4,![]() ,因為
,因為![]() ,所以這個三角形是奇異三角形.
,所以這個三角形是奇異三角形.
(1)根據定義:“等邊三角形是奇異三角形”這個命題是______命題(填“真”或“假命題”);
(2)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 是奇異三角形,求
是奇異三角形,求![]() ;
;
(3)如圖,以![]() 為斜邊分別在
為斜邊分別在![]() 的兩側作直角三角形,且
的兩側作直角三角形,且![]() ,若四邊形
,若四邊形![]() 內存在點
內存在點![]() ,使得
,使得![]() ,
,![]() .
.
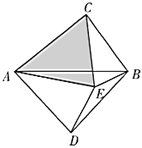
①求證:![]() 是奇異三角形;
是奇異三角形;
②當![]() 是直角三角形時,求
是直角三角形時,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,連接CD、AE交于點F.
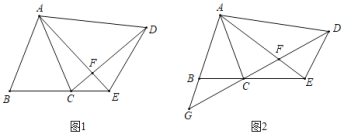
(1)求證:BE=CD.
(2)當∠BAC=∠EAD=30°,AD⊥AB時(如圖2),延長DC、AB交于點G,請直接寫出圖中除△ABC、△ADE以外的等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
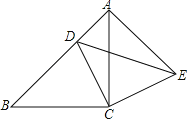
【題目】如圖,△ABC是等腰直角三角形,且∠ACB=90°,點D是AB邊上的一點(點D不與A,B重合),連接CD,過點C作CE⊥CD,且CE=CD,連接DE,AE.
(1)求證:△CBD≌△CAE;
(2)若AD=4,BD=8,求DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com