
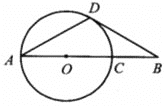
【題目】如圖,線段AB經過圓心O,交⊙O于點A、C,點D在⊙O上,連接AD,BD,∠A=∠B=30°.
證明:(1)BD是⊙O的切線
(2)如果BD=2求OC的長
 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
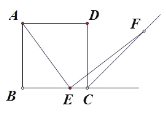
【題目】如圖,四邊形 ABCD 是正方形,點 E是 BC邊上任意一點, AEF 90°,且EF 交正方形外角的平分線 CF 于點 F.求證:AE=EF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB為直徑,AC為弦.過BC延長線上一點G,作GD⊥AO于點D,交AC于點E,交⊙O于點F,M是GE的中點,連接CF,CM.
(1)判斷CM與⊙O的位置關系,并說明理由;
(2)若∠ECF=2∠A,CM=6,CF=4,求MF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的頂點A在x軸負半軸上,頂點C在x軸正半軸上,頂點B在第一象限,線段OA,OC的長是一元二次方程x2-12x+36=0的兩根,BC=4![]() ,∠BAC=45°.
,∠BAC=45°.
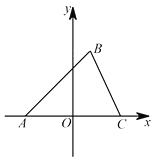
(1)直接寫出點A的坐標________點 C的坐標________;
(2)若反比例函數y=![]() 的圖象經過點B,求k的值;
的圖象經過點B,求k的值;
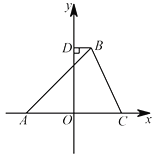
(3)如圖過點B作BD⊥y軸于點D;在y軸上是否存在點P,使以P,B,D為頂點的三角形與以P, O,A為頂點的三角形相似?若存在,直接寫出滿足條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
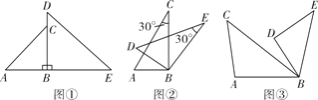
【題目】△ABC和△DBE是繞點B旋轉的兩個相似三角形,其中∠ABC與∠DBE、∠A與∠D為對應角.
(1)如圖①,若△ABC和△DBE分別是以∠ABC與∠DBE為頂角的等腰直角三角形,且兩三角形旋轉到使點B、C、D在同一條直線上的位置時,請直接寫出線段AD與線段EC的關系;
(2)若△ABC和△DBE為含有30°角的直角三角形,且兩個三角形旋轉到如圖②的位置時,試確定線段AD與線段EC的關系,并說明理由;
(3)若△ABC和△DBE為如圖③的兩個三角形,且∠ACB=α,∠BDE=β,在繞點B旋轉的過程中,直線AD與EC夾角的度數是否改變?若不改變,直接用含α、β的式子表示夾角的度數;若改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O的直徑AB為10cm,弦BC為5cm,D、E分別是∠ACB的平分線與⊙O,AB的交點,P為AB延長線上一點,且PC=PE.

(1)求AC、AD的長;
(2)試判斷直線PC與⊙O的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
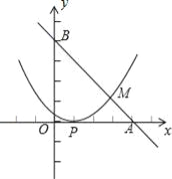
【題目】已知,如圖,直線l經過A(4,0)和B(0,4)兩點,拋物線y=a(x﹣h)2的頂點為P(1,0),直線l與拋物線的交點為M.
(1)求直線l的函數解析式;
(2)若S△AMP=3,求拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是△ABC的內心,AE的延長線和△ABC的外接圓相交于點D.AD與BC相交于點F,連結BE,DC,已知EF=2,CD=5,則AD=______________.

查看答案和解析>>
科目:初中數學 來源: 題型:
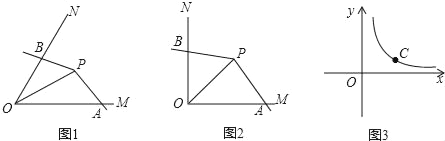
【題目】如圖1,點P為∠MON的平分線上一點,以P為頂點的角的兩邊分別與射線OM,ON交于A,B兩點,如果∠APB繞點P旋轉時始終滿足OAOB=OP2,我們就把∠APB叫做∠MON的智慧角.
(1)如圖2,已知∠MON=90°,點P為∠MON的平分線上一點,以P為頂點的角的兩邊分別與射線OM,ON交于A,B兩點,且∠APB=135°.求證:∠APB是∠MON的智慧角.
(2)如圖1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,連結AB,用含α的式子分別表示∠APB的度數和△AOB的面積.
(3)如圖3,C是函數y=![]() (x>0)圖象上的一個動點,過C的直線CD分別交x軸和y軸于A,B兩點,且滿足BC=2CA,請求出∠AOB的智慧角∠APB的頂點P的坐標.
(x>0)圖象上的一個動點,過C的直線CD分別交x軸和y軸于A,B兩點,且滿足BC=2CA,請求出∠AOB的智慧角∠APB的頂點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com