Question

等邊三角形是大家熟悉的特殊三角形，除了以前我們所知道的它的一些性質(zhì)外，它還有很多其它的性質(zhì)，我們來研究下面的問題：

如圖1，點P是等邊△ABC的中心，PD⊥AB于D，PE⊥BC于E，PF⊥AC于F，易證：BE+CF+AD=EC+AF+BD
問題提出：如圖2，若點P是等邊△ABC內(nèi)任意一點，PD⊥AB于D，PE⊥BC于E，PF⊥AC于F，上述結(jié)論還成立嗎？
為了解決這個問題，現(xiàn)給予證明過程：
證明：連接PA、PB、PC，在Rt△PBE和Rt△PEC中，PB²=PE²+BE²，PC²=PE²+CE²，∴PB²-PC²=BE²-CE²
同理可證：PC²-PA²=CF²-AF²，PA²-PB²=AD²-BD²．
將上述三式相加得：BE²-CE²+CF²-AF²+AD²-BD²=0，即：（BE+CE）（BE-CE）+（CF+AF）（CF-AF）+（AD+BD）（AD-BD）=0
∵△ABC是等邊三角形，設(shè)邊長為a．
∴BE+CE=CF+AF=AD+BD=a；
∴a（BE-CE）+a（CF-AF）+a（AD-BD）=0；
∴BE-CE+CF-AF+AD-BD=0；
∴BE+CF+AD=EC+AF+BD．
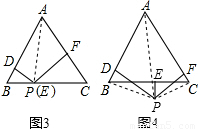
問題拓展：如圖3，若點P是等邊△ABC的邊上任意一點，PD⊥AB于D，PF⊥AC于F，上述結(jié)論還成立嗎？若成立，請直接寫出結(jié)論，不用證明；若不成立，請說明理由．
問題解決：
如圖4，若點P是等邊△ABC外任意一點，PD⊥AB于D，PE⊥BC于E，PF⊥AC于F，上述結(jié)論還成立嗎？若成立，請寫出證明過程；若不成立，請說明理由．

Answer 1

【答案】分析：問題拓展：連接PA，然后根據(jù)“問題提出”的證明思路證明即可；
問題解決：連接PA、PB、PC，然后根據(jù)“問題提出”的證明思路證明即可．
解答：解：問題拓展：BE+CF+AD=EC+AF+BD仍然成立．
理由如下：如圖3，連接PA，在Rt△PAD和Rt△PBD中，PA²=AD²+PD²，PB²=BD²+PD²，
∴PA²-PB²=AD²-BD²，
同理可證：PC²-PA²=CF²-AF²，
又∵PB²=BE²，PC²=CE²，
∴PB²-PC²=BE²-CE²，
將上述三式相加得：AD²-BD²+CF²-AF²+BE²-CE²=0，
即：（BE+CE）（BE-CE）+（CF+AF）（CF-AF）+（AD+BD）（AD-BD）=0，
∵△ABC是等邊三角形，設(shè)邊長為a，
∴BE+CE=CF+AF=AD+BD=a，
∴a（BE-CE）+a（CF-AF）+a（AD-BD）=0，
∴BE-CE+CF-AF+AD-BD=0，
∴BE+CF+AD=EC+AF+BD；

問題解決：如圖4，連接PA、PB、PC，
在Rt△PBE和Rt△PEC中，PB²=PE²+BE²，PC²=PE²+CE²，
∴PB²-PC²=BE²-CE²，
同理可證：PC²-PA²=CF²-AF²，PA²-PB²=AD²-BD²，
將上述三式相加得：BE²-CE²+CF²-AF²+AD²-BD²=0，
即：（BE+CE）（BE-CE）+（CF+AF）（CF-AF）+（AD+BD）（AD-BD）=0，
∵△ABC是等邊三角形，設(shè)邊長為a，
∴BE+CE=CF+AF=AD+BD=a，
∴a（BE-CE）+a（CF-AF）+a（AD-BD）=0，
∴BE-CE+CF-AF+AD-BD=0，
∴BE+CF+AD=EC+AF+BD．
點評：本題考查了等邊三角形的性質(zhì)，勾股定理的應(yīng)用，讀懂題目信息，理解證明思路與方法是解題的關(guān)鍵．