
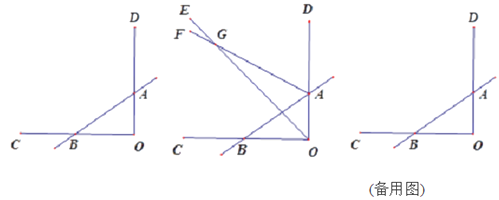
【題目】已知如圖,∠COD=90°,直線AB與OC交于點B,與OD交于點A,射線OE與射線AF交于點G.
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=42°,則∠OGA= ;
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=42°,則∠OGA= ;
∠BAD,∠OBA=42°,則∠OGA= ;
(3)將(2)中的“∠OBA=42°”改為“∠OBA=![]() ”,其它條件不變,求∠OGA的度數.(用含
”,其它條件不變,求∠OGA的度數.(用含![]() 的代數式表示)
的代數式表示)
(4)若OE將∠BOA分成1︰2兩部分,AF平分∠BAD,∠ABO=![]() (30°<
(30°<![]() <90°) ,求∠OGA的度數.(用含
<90°) ,求∠OGA的度數.(用含![]() 的代數式表示)
的代數式表示)
【答案】(1)∠OGA=21°;
(2)∠OGA=14°;
(3)∠OGA=![]() ;
;
(4)∠OGA的度數為![]() 或
或![]()
【解析】試題分析:(1)根據三角形外角的性質求出∠BAD,求出∠GOA和∠GAD,根據三角形外角性質求出即可;(2)根據三角形外角的性質求出∠BAD,求出∠GOA和∠GAD,根據三角形外角性質求出即可;(3)根據三角形外角的性質求出∠BAD,求出∠GOA和∠GAD,根據三角形外角性質求出即可;(4)討論:當∠EOD:∠COE=1:2時,利用∠BAD=∠ABO+∠BOA=β+90°,∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=β+90°,則∠OGA=![]() β+15°;當∠EOD:∠COE=2:1時,則∠EOD=60°,同理得∠OGA=
β+15°;當∠EOD:∠COE=2:1時,則∠EOD=60°,同理得∠OGA=![]() β-15°.
β-15°.
試題解析:(1)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵AF平分∠BAD,OE平分∠BOA,∠BOA=90°,
∴∠GAD=![]() ∠BAD=66°,∠EOA=
∠BAD=66°,∠EOA=![]() ∠BOA=45°,
∠BOA=45°,
∴∠OGA=∠GAD∠EOA=66°45°=21°;
故答案為21°;
(2)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵∠BOA=90°,∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD
∠BAD
∴∠GAD=44°,∠EOA=30°,
∴∠OGA=∠GAD∠EOA=44°30°=14°;
故答案為14°;
(3)∵∠BOA=90°,∠OBA=α,
∴∠BAD=∠BOA+∠ABO=90°+α,
∵∠BOA=90°,∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD
∠BAD
∴∠GAD=30°+![]() α,∠EOA=30°,
α,∠EOA=30°,
∴∠OGA=∠GAD∠EOA=![]() α,
α,
故答案為:![]() α;
α;
(4)當∠EOD:∠COE=1:2時,
則∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=α+90°,
∵AF平分∠BAD,
∴∠FAD=![]() ∠BAD,
∠BAD,
∵∠FAD=∠EOD+∠OGA,
∴2×30°+2∠OGA=α+90°,
∴∠OGA=![]() α+15°;
α+15°;
當∠EOD:∠COE=2:1時,則∠EOD=60°,
同理得到∠OGA=![]() α15°,
α15°,
即∠OGA的度數為![]() α+15°或
α+15°或![]() α15°.
α15°.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:
【題目】已知:關于![]() 的一元二次方程
的一元二次方程![]() ,
,
(1)求證:方程有兩個不相等的實數根且其中一個根為定值。
(2)設方程的兩個實數根分別為![]() ,
, ![]() (其中
(其中![]() <
<![]() )。若y是關于m的函數,且
)。若y是關于m的函數,且![]() ,求這個函數的解析式;并求當自變量
,求這個函數的解析式;并求當自變量![]() 的取值范圍滿足什么條件時,
的取值范圍滿足什么條件時, ![]() 。
。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列各式,能用平方差公式計算的是( )
A.(-a+b)(b-a)
B.(2x+1)(-2x-1)
C.(-5y+3)(5y+3)
D.(-2m+n)(2m-n)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=ax+b與反比例函數y=![]() (x>0)的圖象交于A(1,4),B(4,n)兩點,與x軸,y軸分別交干C,D兩點.
(x>0)的圖象交于A(1,4),B(4,n)兩點,與x軸,y軸分別交干C,D兩點.

(1)m= ,n= ;若M(xl,y1),N(x2,y2)是反比例函數圖象上兩點,且0<xl<x2,則yl y2(填“<”或“=”或“>”);
(2)若線段CD上的點P到x軸,y軸的距離相等.求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果將三角形ABC三個頂點的橫坐標都減2,縱坐標都加6,得到三角形A′B′C′,則三角形A′B′C′是由三角形ABC先向____平移____個單位長度,再向____平移____個單位長度得到.
查看答案和解析>>
科目:初中數學 來源: 題型:
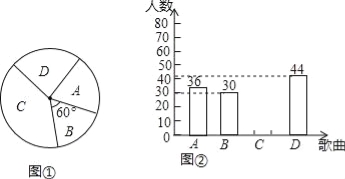
【題目】為慶祝建黨95周年,某校團委計劃在“七一”前夕舉行“唱響紅歌”班級歌詠比賽,要確定一首喜歡人數最多的歌曲為每班必唱歌曲.為此提供代號為A,B,C,D四首備選曲目讓學生選擇,經過抽樣調查,并將采集的數據繪制如下兩幅不完整的統計圖.請根據圖①,圖②所提供的信息,解答下列問題:
(1)本次抽樣調查中,選擇曲目代號為A的學生占抽樣總數的百分比為 ;
(2)請將圖②補充完整;
(3)若該校共有1530名學生,根據抽樣調查的結果估計全校共有多少學生選擇此必唱歌曲?(要有解答過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,有若干張邊長為![]() 的小正方形①、長為
的小正方形①、長為![]() 寬為
寬為![]() 的長方形②以及邊長為
的長方形②以及邊長為![]() 的大正方形③的紙片.
的大正方形③的紙片.
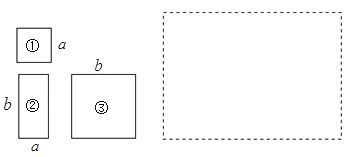
(1)已知小正方形①與大正方形③的面積之和為169,長方形②的周長為34,求長方形②的面積.
(2)如果現有小正方形①1張,大正方形③2張,長方形②3張,請你將它們拼成一個大長方形 (在圖2虛線框內畫出圖形),并運用面積之間的關系,將多項式![]() 分解因式.
分解因式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com