【題目】對于一元二次方程
，有下列說法：
①若
，則方程必有一個根為1；
②若方程
有兩個不相等的實根，則方程必有兩個不相等的實根；
③若
是方程的一個根，則一定有
成立；
④若
是一元二次方程的根，則
．
其中正確的有（ ）
A.1個B.2個C.3個D.4個
【答案】A
【解析】
按照方程的解的含義、一元二次方程的實數根與判別式的關系、等式的性質、一元二次方程的求根公式等對各選項分別討論，可得答案．
解：①若x=1時，方程ax2+bx+c=0，則a+b+c=0，
∵無法確定a-b+c=0．故①錯誤；
②∵方程ax2+c=0有兩個不相等的實根，
∴△=0-4ac＞0
∴-4ac＞0
則方程ax2+bx+c=0的判別式，
△=b2-4ac＞0
∴方程ax2+bx+c=0必有兩個不相等的實根，故②正確；
③∵c是方程ax2+bx+c=0的一個根，
則ac2+bc+c=0
∴c（ac+b+1）=0
若c=0，等式仍然成立，
但ac+b+1=0不一定成立，故③錯誤；
④若x0是一元二次方程ax2+bx+c=0的根，
則由求根公式可得：
或
，
∴
或
∴b24ac＝(2ax0+b)2，故④錯誤．
故選：A．
奪冠金卷全能練考系列答案科目：初中數學 來源： 題型：
【題目】觀察下列等式：
（a﹣b）（a+b）＝a2﹣b2
（a﹣b）（a2+ab+b2）＝a3﹣b3
（a﹣b）（a3+a2b+ab2+b3）＝a4﹣b4…
利用你的發現的規律解決下列問題
（1）（a﹣b）（a4+a3b+a2b2+ab3+b4）＝ （直接填空）；
（2）（a﹣b）（an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1）＝ （直接填空）；
（3）利用（2）中得出的結論求62019+62018+…+62+6+1的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
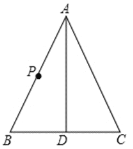
【題目】如圖，在△ABC中，AB＝AC， AD是△ABC 底邊BC上的中線，P為AB上一點．
（1）在AD上找一點E，使得PE+EB的值最小；
（2）若P為AB的中點，當∠BPE＝ °時，△ABC是等邊三角形．（直接寫出結果）
查看答案和解析>>
科目：初中數學 來源： 題型：
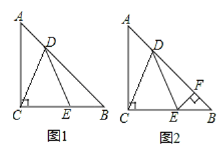
【題目】△ABC中，AC＝BC，∠ACB＝90°，點D在AB上，E在BC上，且AD＝BE，BD＝AC．
（1）如圖1，求證：DC＝DE；
（2）如圖2，過E作EF⊥AB于F，若BF＝2，求CE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】世界上大部分國家都使用攝氏溫度(
)，但美國、英國等國家的天氣預報仍然使用華氏溫度(
).兩種計量之間有如下對應：
攝氏溫度( |
|
|
|
|
|
|
華氏溫度( |
|
|
|
|
|
|
(1)上表反映了哪兩變量之間的關系？哪個是自變量？哪個是因變量？
(2)由上表可得：攝氏溫度()每提高
度，華氏溫度()提高_____度.
(3)攝氏溫度
度時華氏溫度為______度.
(4)華氏溫度
度時攝氏溫度為_______度.
(5)華氏溫度的值與對應的攝氏溫度的值有相等的可能嗎？如果有，求出這個值.如果沒有，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，連接BD，且BD＝CD，過點A作AM⊥BD于點M，過點D作DN⊥AB于點N，且DN＝
，在DB的延長線上取一點P，滿足∠ABD＝∠MAP＋∠PAB，則AP＝_____.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料I：教材中我們學習了:若關于
的一元二次方程
的兩根為
，根據這一性質，我們可以求出己知方程關于
的代數式的值．
問題解決:
（1）已知為方程
的兩根，則
，
，那么
.(請你完成以上的填空)
閱讀材料II：已知
，且
．求
的值．
解:由
可知
又
且，即
是方程
的兩根．
問題解決:
（2）已知
且．求
的值；
，則
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
