
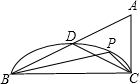
 如圖,以△ABC的邊BC為弦,在點A的同側畫
如圖,以△ABC的邊BC為弦,在點A的同側畫 交AB于D,且∠BDC=90°+
交AB于D,且∠BDC=90°+ ∠A,點P是
∠A,點P是 上的一個動點.
上的一個動點. 上運動時,過點P畫直線MN⊥AP,分別交AB、AC于點M、N,是否存在這樣的點P,使得△BMP和△BPC和△CPN彼此相似?請說明理由.
上運動時,過點P畫直線MN⊥AP,分別交AB、AC于點M、N,是否存在這樣的點P,使得△BMP和△BPC和△CPN彼此相似?請說明理由.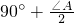 ,
,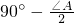 ,
,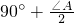 -∠A=
-∠A=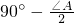 ,
,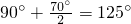 ,
, 的中點時,△BMP和△BPC和△CPN彼此相似.
的中點時,△BMP和△BPC和△CPN彼此相似. 的中點,
的中點,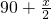 )=90-y-
)=90-y- ,
, )=90-y-
)=90-y- ,
, 的中點時,點P是△ABC的角平分線的交點.
的中點時,點P是△ABC的角平分線的交點. =∠BPC,
=∠BPC, 的中點時,△BMP和△BPC和△CPN彼此相似,可得∠ABP=∠CBP,即可設∠A=x度,∠ABP=∠CBP=y度,利用方程表達可得∠PCB=∠ACP,即可得到∠BMP=∠CNP=90+
的中點時,△BMP和△BPC和△CPN彼此相似,可得∠ABP=∠CBP,即可設∠A=x度,∠ABP=∠CBP=y度,利用方程表達可得∠PCB=∠ACP,即可得到∠BMP=∠CNP=90+ =∠BPC,問題得證.
=∠BPC,問題得證.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 26、如圖,以△ABC的邊AB、AC為邊的等邊三角ABD和等邊三角形ACE,四邊形ADFE是平行四邊形.
26、如圖,以△ABC的邊AB、AC為邊的等邊三角ABD和等邊三角形ACE,四邊形ADFE是平行四邊形.查看答案和解析>>
科目:初中數學 來源: 題型:
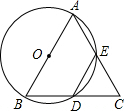 如圖,以△ABC的邊AB為直徑作⊙O,交BC于D點,交AC于E點,BD=DE
如圖,以△ABC的邊AB為直徑作⊙O,交BC于D點,交AC于E點,BD=DE | BD |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2011•峨眉山市二模)如圖,以△ABC的邊AB為直徑作⊙O,BC與⊙O交于D,D是BC的中點,過D作DE⊥AC,交AC于點E.
(2011•峨眉山市二模)如圖,以△ABC的邊AB為直徑作⊙O,BC與⊙O交于D,D是BC的中點,過D作DE⊥AC,交AC于點E.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2010•黔東南州)如圖,以△ABC的邊BC為直徑作⊙O分別交AB,AC于點F.點E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔東南州)如圖,以△ABC的邊BC為直徑作⊙O分別交AB,AC于點F.點E,AD⊥BC于D,AD交于⊙O于M,交BE于H.查看答案和解析>>
科目:初中數學 來源: 題型:
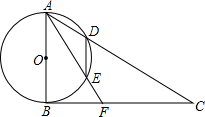 如圖,以△ABC的邊AB為直徑的⊙O交AC于點D,弦DE∥AB,∠C=∠BAF
如圖,以△ABC的邊AB為直徑的⊙O交AC于點D,弦DE∥AB,∠C=∠BAF| 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com