

 ,你能用矩形的性質說明這個結論嗎?請說明.
,你能用矩形的性質說明這個結論嗎?請說明.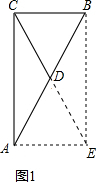 證明:(1)如圖,延長CD至點E,使CD=DE,連接AE、BE,
證明:(1)如圖,延長CD至點E,使CD=DE,連接AE、BE, CE,
CE, AB;
AB;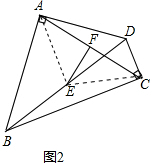 .理由如下:
.理由如下: DB,
DB, BD,
BD,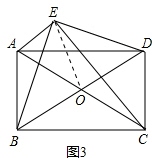
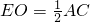 ,
,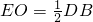 ,
, AB;
AB; DB,OE=
DB,OE= AC,進而得到AC=BD,根據對角線相等的平行四邊形是矩形可得結論.
AC,進而得到AC=BD,根據對角線相等的平行四邊形是矩形可得結論.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
 教育部制定《數學課程標準》要求的課程目標之一是通過數學學習,學生能夠“初步學會運用數學的思維方式去觀察、分析現實社會,去解決日常生活中和其他學科學習中的問題,增強應用數學的意識.”
教育部制定《數學課程標準》要求的課程目標之一是通過數學學習,學生能夠“初步學會運用數學的思維方式去觀察、分析現實社會,去解決日常生活中和其他學科學習中的問題,增強應用數學的意識.”查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 教育部制定《數學課程標準》要求的課程目標之一是通過數學學習,學生能夠“初步學會運用數學的思維方式去觀察、分析現實社會,去解決日常生活中和其他學科學習中的問題,增強應用數學的意識.”
教育部制定《數學課程標準》要求的課程目標之一是通過數學學習,學生能夠“初步學會運用數學的思維方式去觀察、分析現實社會,去解決日常生活中和其他學科學習中的問題,增強應用數學的意識.”查看答案和解析>>
科目:初中數學 來源:競賽題 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com