
【題目】如圖,已知二次函數![]() 的圖像與x軸交于A、B兩點(點A在點B左側),與y軸交于點C.
的圖像與x軸交于A、B兩點(點A在點B左側),與y軸交于點C.
(1)求線段BC的長;
(2)當0≤y≤3時,請直接寫出x的范圍;
(3)點P是拋物線上位于第一象限的一個動點,連接CP,當∠BCP=90o時,求點P的坐標.
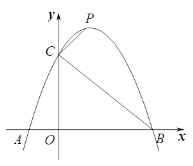
【答案】(1)5 ;(2)![]() ,
,![]() ;(3)點P坐標為(
;(3)點P坐標為(![]() ,
,![]() ).
).
【解析】
(1)分別求出點B和點C的坐標,再運用勾股定理即可求出BC的長;
(2)求出y=0和y=3時相應的x的值,結合函數的圖象即可得到答案;
(3)過點P作PD⊥y軸,設點P坐標為(x, ![]() ),則點D坐標為(0,
),則點D坐標為(0, ![]() ),表示出PD,CD,證明△PDC∽△COB,得出
),表示出PD,CD,證明△PDC∽△COB,得出![]() ,列方程求解即可.
,列方程求解即可.
(1)當x=0時,y=3,
∴C(0,3),
∴OC=3
當y=0時![]() ,解得x1=-1,x2=4
,解得x1=-1,x2=4
∴A(-1,0),B(4,0),
∴OA=1,OB=4
在Rt△BOC中,BC=![]() =5;
=5;
(2) 當y=0時![]() ,解得x1=-1,x2=4
,解得x1=-1,x2=4
當y=3時![]() ,解得x1=0,x2=4
,解得x1=0,x2=4
∴當0≤y≤3時,![]() ,
,![]()
(3)過點P作PD⊥y軸
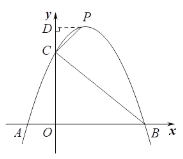
設點P坐標為(x, ![]() ),則點D坐標為(0,
),則點D坐標為(0, ![]() )
)
∴PD=x,CD=![]() -3=
-3=![]() /p>
/p>
∵∠BCP=90°,
∴∠PCD+∠BCO=90°,
∵∠PCD+∠CPD=90°,
∴∠BCO=∠CPD
∵∠PDC=∠BOC=90°,
∴△PDC∽△COB
∴![]() ,
,
∴![]() ,
,
∴x=![]() 或x=0(舍去)
或x=0(舍去)
當x=![]() 時,y=
時,y=![]()
∴點P坐標為(![]() ,
,![]() ).
).


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:初中數學 來源: 題型:
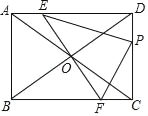
【題目】如圖,在矩形ABCD中,AB=3,BC=4,將對角線AC繞對角線交點O旋轉,分別交邊AD、BC于點E、F,點P是邊DC上的一個動點,且保持DP=AE,連接PE、PF,設AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代數式表示)
(2)求△PEF面積的最小值;
(3)在運動過程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
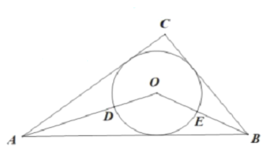
【題目】如圖,在Rt![]() ABC中,∠C=90
ABC中,∠C=90![]() ,AC=8,BC=6,
,AC=8,BC=6,![]() O為ABC的內切圓,OA,OB與
O為ABC的內切圓,OA,OB與![]() O分別交于點D,E,則劣弧DE的長是________.
O分別交于點D,E,則劣弧DE的長是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強學生的身體素質,教育行政部門規定學生每天參加戶外活動的平均時間不少于1小時,為了解學生參加戶外活動的情況,對部分學生參加戶外活動的時間進行抽樣調查,并將調查結果繪制作成如下兩幅不完整的統計圖,請你根據圖中提供的信息解答下列問題:
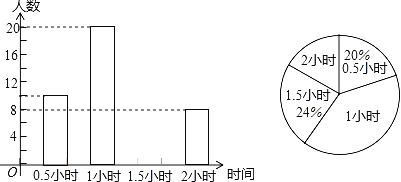
(1)在這次調查中共調查了多少名學生;
(2)求戶外活動時間為1.5小時的人數,并補充頻數分布直方圖;
(3)求戶外活動時間的眾數和中位數是多少;
(4)本次調查中學生參加戶外活動的平均時間是否符合要求,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為滿足市場需求,新生活超市在端午節前夕購進價格為![]() 元/個的粽子,根據市場預測,該品牌粽子每個售價
元/個的粽子,根據市場預測,該品牌粽子每個售價![]() 元時,每天能出售
元時,每天能出售![]() 個,并且售價每上漲
個,并且售價每上漲![]() 元,其銷售量將減少
元,其銷售量將減少![]() 個,為了維護消費者利益,物價部門規定,該品牌粽子的售價不能超過進價的
個,為了維護消費者利益,物價部門規定,該品牌粽子的售價不能超過進價的![]() .
.
(1)請你利用所學知識幫助超市給該品牌粽子定價,使超市每天的銷售利潤為![]() 元.
元.
(2)定價為多少時每天的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
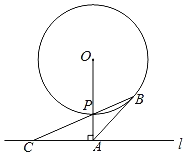
【題目】如圖,直線l與⊙O相離,OA⊥![]() 于點A,與⊙O相交于點P,OA=5.C是直線
于點A,與⊙O相交于點P,OA=5.C是直線![]() 上一點,連結CP并延長交⊙O于另一點B,且AB=AC.
上一點,連結CP并延長交⊙O于另一點B,且AB=AC.
(1)求證:AB是⊙O的切線;
(2)若⊙O的半徑為3,求線段BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一茶葉專賣店經銷某種品牌的茶葉,該茶葉的成本價是80元/kg,銷售單價不低于120元/kg,且不高于180元/kg,經銷一段時間后得到如下數據:

設y與x的關系是我們所學過的某一種函數關系.
(1)寫出y與x的函數關系式,并指出自變量x的取值范圍;
(2)當銷售單價為多少時,銷售利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年5月的第二個星期日即為母親節,“父母恩深重,恩憐無歇時”,許多市民喜歡在母親節為母親送花,感恩母親,祝福母親.今年節日前夕,某花店采購了一批康乃馨,經分析上一年的銷售情況,發現這種康乃馨每天的銷售量y(支)是銷售單價x(元)的一次函數,已知銷售單價為7元/支時,銷售量為16支;銷售單價為8元/支時,銷售量為14支.
(1)求這種康乃馨每天的銷售量y(支)關于銷售單價x(元/支)的一次函數解析式;
(2)若按去年方式銷售,已知今年這種康乃馨的進價是每支5元,商家若想每天獲得42元的利潤,銷售單價要定為多少元?
(3)在(2)的條件下,當銷售單價x為何值時,花店銷售這種康乃馨每天獲得的利潤最大?并求出獲得的最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com