
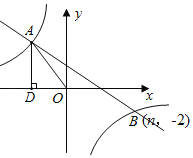
【題目】如圖所示,在平面直角坐標系中,一次函數y=kx+b(k≠0)與反比例函數y=![]() (m≠0)的圖象交于第二、四象限A、B兩點,過點A作AD⊥x軸于D,AD=4,sin∠AOD=
(m≠0)的圖象交于第二、四象限A、B兩點,過點A作AD⊥x軸于D,AD=4,sin∠AOD=![]() ,且點B的坐標為(n,-2).
,且點B的坐標為(n,-2).
(1)求一次函數與反比例函數的解析式;
(2)E是y軸上一點,且△AOE是等腰三角形,請直接寫出所有符合條件的E點坐標.
【答案】(1)![]() ;(2)當點E(0,8)或(0,5)或(0,-5)或(0,
;(2)當點E(0,8)或(0,5)或(0,-5)或(0,![]() )時,△AOE是等腰三角形.
)時,△AOE是等腰三角形.
【解析】
(1)由垂直的定義及銳角三角函數定義求出AO的長,利用勾股定理求出OD的長,確定出A坐標,進而求出m的值確定出反比例解析式,把B的坐標代入反比例解析式求出n的值,確定出B坐標,利用待定系數法求出一次函數解析式即可;
(2)分類討論:當AO為等腰三角形腰與底時,求出點E坐標即可.
(1)![]() 一次函數
一次函數![]() 與反比例函數
與反比例函數![]() 圖象交于
圖象交于![]() 與
與![]() ,且
,且![]() 軸,
軸,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]()
![]() ,即
,即![]() ,
,
根據勾股定理得:![]() ,
,
![]() ,
,
代入反比例解析式得:![]() ,即
,即![]() ,
,
把![]() 坐標代入得:
坐標代入得:![]() ,即
,即![]() ,
,
代入一次函數解析式得:![]() ,
,
解得: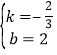 ,即
,即![]() ;
;
(2)當![]() ,即
,即![]() ,
,![]() ;
;
當![]() 時,得到
時,得到![]() ,即
,即![]() ;
;
當![]() 時,由
時,由![]() ,
,![]() ,得到直線
,得到直線![]() 解析式為
解析式為![]() ,中點坐標為
,中點坐標為![]() ,
,
![]() 垂直平分線方程為
垂直平分線方程為![]() ,
,
令![]() ,得到
,得到![]() ,即
,即![]() ,
,
綜上,當點![]() 或
或![]() 或
或![]() 或
或![]() 時,
時,![]() 是等腰三角形.
是等腰三角形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
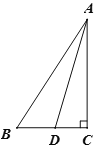
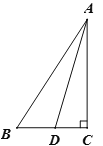
【題目】如圖,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分線EF交AD于點E,交BC的延長線于點F,交AB于點G,交AC于點H.
(1)依題意補全圖形;
(2)求證:∠BAD=∠BFG;
(3)試猜想AB,FB和FD之間的數量關系并進行證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c的對稱軸是x=﹣1,且過點(![]() ,0),有下列結論:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有錯誤的結論有( )個.
,0),有下列結論:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有錯誤的結論有( )個.
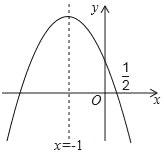
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,將一個量角器與一張等邊三角形(△ABC)紙片放置成軸對稱圖形,CD⊥AB,垂足為D,半圓(量角器)的圓心與點D重合,此時,測得頂點C到量角器最高點的距離CE=2cm,將量角器沿DC方向平移1cm,半圓(量角器)恰與△ABC的邊AC,BC相切,如圖2,則AB的長為__________cm.
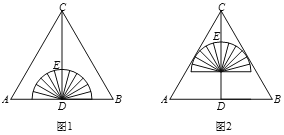
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ ABC中,∠ACB=90°,AD平分∠BAC, 作AD的垂直平分線EF交AD于點E,交BC的延長線于點F,交AB于點G,交AC于點H.
(1)依題意補全圖形;
(2)求證:∠BAD=∠BFG;
(3)試猜想AB,FB和FD之間的數量關系并進行證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表顯示的是某種大豆在相同條件下的發芽試驗結果:
每批粒數n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
發芽的粒數m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
發芽的頻率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三個推斷:
①當n為400時,發芽的大豆粒數為382,發芽的頻率為0.955,所以大豆發芽的概率是0.955;
②隨著試驗時大豆的粒數的增加,大豆發芽的頻率總在0.95附近擺動,顯示出一定的穩定性,可以估計大豆發芽的概率是0.95;
③若大豆粒數n為4000,估計大豆發芽的粒數大約為3800粒.
其中推斷合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】公交總站(A點)與B、C兩個站點的位置如圖所示,已知AC=6km,∠B=30°,∠C=15°,求B站點離公交總站的距離即AB的長(結果保留根號).
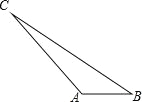
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com