
【題目】如圖(1)所示,A,E,F,C在一條直線上,AE=CF,過E,F分別作DE⊥AC,BF⊥AC,若AB=CD,求證EG=FG.(提示:先證△ABF≌△CDE,得BF=DE,再證△BFG≌△DEG);若將△DEC的邊EC沿AC方向移動,變為圖(2)時,其余條件不變,上述結論是否成立?請說明理由.

科目:初中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,已知AD∥BC,AB=CD,延長線段CB到E,使BE=AD,連接AE、AC.
【1】求證:△ABE≌△CDA;
【2】若∠DAC=40°,求∠EAC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列一段話,并解決后面的問題 .觀察下面一例數:
1,2,4,8,……
我們發現,這一列數從第2項起,每一項與它前一項的比都等于2 .
一般地,如果一列數從第2項起,每一項與它前一項的比都等于同一個常數,這一列數就叫做等比數列,這個常數叫做等比數列的公比 .
(1)等比數列5,-15,45,……的第4項是 ;
(2)如果一列數![]() ,
,![]() ,
,![]() ,
,![]() ,……是等比數列,且公比為q,那么根據上述的規定,有
,……是等比數列,且公比為q,那么根據上述的規定,有
![]() ,
,![]() ,
,![]() ,……
,……
所以![]() ,
,
![]() ,
,
![]() ,
,
……
![]() .(用
.(用![]() 與q的代數式表示)
與q的代數式表示)
(3)一個等比數列的第2項是10,第3項是20,求它的第1項與第4項 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在四邊形ABCD中,∠A=90°.若AB=4cm,AD=3cm,CD=12cm,BC=13cm,
(1)請說明BD⊥CD;
(2)求四邊形ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】李老師為了了解學生暑期在家的閱讀情況,隨機調查了20名學生某一天的閱讀小時數,具體情況統計如下:
閱讀時間 (小時) | 2 | 2.5 | 3 | 3.5 | 4 |
學生人數(名) | 1 | 2 | 8 | 6 | 3 |
則關于這20名學生閱讀小時數的說法正確的是( )
A. 眾數是8 B. 中位數是3 C. 平均數是3 D. 方差是0.34
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家住房結構如圖所示,圖中標了有關尺寸(墻體厚度忽略不計,單位:米)房屋的主人計劃把臥室以外的地面都鋪上地磚.
(1)如果他選用地磚的價格是 a 元/平方米,則買地磚至少需用多少元(圖中標了有關尺寸(墻體厚度忽略不計,單位:米)
(2)如果房屋的高度為 h 米,現需要在客廳和臥室的墻上貼壁紙,至少需要多少平方米的壁紙?(計算時不扣除門、窗所占的面積,結果用代數式表示)?

查看答案和解析>>
科目:初中數學 來源: 題型:
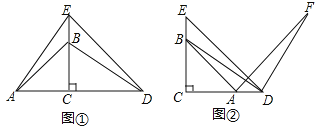
【題目】已知△ABC與△DEC是兩個大小不同的等腰直角三角形.
(1)如圖①所示,連接AE,DB,試判斷線段AE和DB的數量和位置關系,并說明理由;
(2)如圖②所示,連接DB,將線段DB繞D點順時針旋轉90°到DF,連接AF,試判斷線段DE和AF的數量和位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 是正方形
是正方形![]() 內一點,以點
內一點,以點![]() 為旋轉中心,將
為旋轉中心,將![]() 按順時針方向旋轉使點
按順時針方向旋轉使點![]() 與點
與點![]() 重合,這時
重合,這時![]() 點旋轉到
點旋轉到![]() 點.
點.

![]() 設
設![]() 的長為
的長為![]() ,
,![]() 的長為
的長為![]() ,在圖中用陰影標出
,在圖中用陰影標出![]() 旋轉到
旋轉到![]() 的過程中,邊
的過程中,邊![]() 所掃過區域的面積,并用含
所掃過區域的面積,并用含![]() 、
、![]() 的式子表示它________;
的式子表示它________;
![]() 若
若![]() ,
,![]() ,
,![]() ,連接
,連接![]() ,試猜想
,試猜想![]() 的形狀,并說明理由.
的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E,N,P,G分別在邊AB,BC,CD,DA上,點M,F,Q都在對角線BD上,且四邊形MNPQ和AEFG均為正方形,則![]() 的值等于_____.
的值等于_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com