Question

如圖：已知點C在圓O上，P是圓O外一點；割線PO交圓O于點B、A，已知AC=PC，∠COB=2∠PCB，且PB=2；
（1）求證：PC是圓O的切線；
（2）求tan∠P；
（3）M是圓O的下半圓弧上的一動點，當M點運動到使△ABM的面積最大時，過CM的直線交AB于點N，求MN，MC的值．

Answer 1

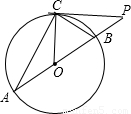
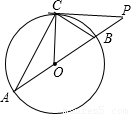
（1）證明：∵∠COB=2∠A，∠COB=2∠PCB，
∴∠PCB=∠A．
∵OC=OA，
∴∠A=∠OCA．
∴∠PCB=∠OCA．
∵AB是直徑，
∴∠OCA+∠BCO=90°．
∴∠PCB+∠BCO=90°．
∴∠OCP=90°．
∴PC是圓O的切線．

（2）解：∵AC=PC，
∴∠P=∠A．
設∠A=x°，則∠PCB=∠P=∠OCA=x°，
∴∠COB=2∠PCB=2x°，∠CBO=∠P+∠PCB=2x°．
∵OB=OC，
∴∠OCB=∠OBC=2x°．
∴x=30°，tan∠P=．

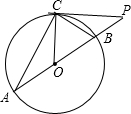
（3）解：在Rt△OCP中，
∵∠OPC=30°，
∴OP=2OC．
∵PB=2，
∴OC=OB=2．
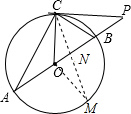
∴OP=4，PC=2．
過O作OM⊥AB于O，則△ABM的面積最大．
∵∠COM=150°，OC=OM，
∴∠M=∠OCM=15°．
∴∠PNC=75°，
∴∠PCN=∠OCP-∠OCM=75°．
∴PN=PC=2．
∴ON=2+4．
∵OM=2，
∴MN=2+2．
又∵NB•NA=NC•NM，
∴NC=+3．
∴MC=MN-NC=-．
∴MN=2+2，MC=-．
分析：（1）根據切線的判定定理，證明∠OCP=90°即可；
（2）根據條件容易求出∠P=30°；
（3）因為AB是定值，所以當OM⊥AB時，AB邊上的高最大，則△ABM的面積最大，則M點的位置確定，N的位置也隨之確定，又OM的值已求，ON的值易求，從而可根據勾股定理在Rt△OMN中求出MN的值，再由割線定理求出NC，然后根據MC=MN-NC求出MC的值．
點評：本題考查切線的判定，三角函數，切割線定理，勾股定理的綜合運用．