
【題目】如圖![]() ,已知直線
,已知直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,以
兩點,以![]() 為直角頂點在第二象限作等腰
為直角頂點在第二象限作等腰![]() .
.
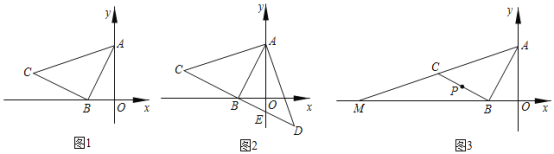
(1)求點![]() 的坐標,并求出直線
的坐標,并求出直線![]() 的關系式;
的關系式;
(2)如圖![]() ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,在直線
,在直線![]() 上取一點
上取一點![]() ,連接
,連接![]() ,若
,若![]() ,求證:
,求證:![]() .
.
(3)如圖![]() ,在(1)的條件下,直線
,在(1)的條件下,直線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() 是線段
是線段![]() 上一點,在
上一點,在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使
,使![]() 面積等于
面積等于![]() 面積的一半?若存在,請求出點
面積的一半?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)y=![]() x+4;(2)見解析;(3)存在,點N(﹣
x+4;(2)見解析;(3)存在,點N(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)根據題意證明△CHB≌△BOA(AAS),即可求解;
(2)求出B、E、D的坐標分別為(-1,0)、(0,![]() )、(1,-1),即可求解;
)、(1,-1),即可求解;
(3)求出BC表達式,將點P代入,求出a值,再根據AC表達式求出M點坐標,由S△BMC=![]() MB×yC=
MB×yC=![]() ×10×2=10,S△BPN=
×10×2=10,S△BPN=![]() S△BCM=5=
S△BCM=5=![]() NB×a=
NB×a=![]() 可求解.
可求解.
解:(1)令x=0,則y=4,令y=0,則x=﹣2,
則點A、B的坐標分別為:(0,4)、(﹣2,0),
過點C作CH⊥x軸于點H,
∵∠HCB+∠CBH=90°,∠CBH+∠ABO=90°,
∴∠ABO=∠BCH,
∠CHB=∠BOA=90°,BC=BA,
在△CHB和△BOA中,
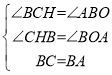 ,
,
∴△CHB≌△BOA(AAS),
∴BH=OA=4,CH=OB=2,
∴ 點C(﹣6,2),
將點A、C的坐標代入一次函數表達式:y= m x+ b得:![]() ,
,
解得: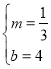 ,
,
故直線AC的表達式為:y=![]() x+4;
x+4;
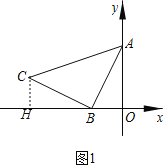
(2)同理可得直線CD的表達式為:y=﹣![]() x﹣1①,則點E(0,﹣1),
x﹣1①,則點E(0,﹣1),
直線AD的表達式為:y=﹣3x+4②,
聯立①②并解得:x=2,即點D(2,﹣2),
點B、E、D的坐標分別為(﹣
故點E是BD的中點,即BE=DE;
(3)將點BC的坐標代入一次函數表達式并解得:
直線BC的表達式為:y=﹣![]() x-1,
x-1,
將點P(﹣![]() ,a)代入直線BC的表達式得:
,a)代入直線BC的表達式得:![]() ,
,
直線AC的表達式為:y=![]() x+4,
x+4,
令y=0,則x=-12,則點M(﹣12,0),
S△BMC=![]() MB×y C=
MB×y C=![]() ×10×2=10,
×10×2=10,
S△BPN=![]() S△BCM=5=
S△BCM=5=![]() NB×a=
NB×a=![]() ,
,
解得:NB=![]() ,
,
故點N(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=-x2+2x+3與x軸相交于A、B兩點(點A在點B的左側),與y軸相交于點C,頂點為D.
(1)求出A、B、C三點的坐標和拋物線的對稱軸;
(2)連接BC,與拋物線的對稱軸交于點E,點P為線段BC上的一個動點,過點P作PF∥DE交拋物線于點F,設點P的橫坐標為m;
①用含m的代數式表示線段PF的長,并求出當m為何值時,四邊形PEDF為平行四邊形?
②設△BCF的面積為S,求S與m的函數關系式,S是否有最大值?如有,請求出最大值,沒有請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
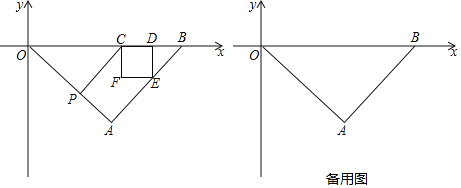
【題目】如圖,平面直角坐標系中,點A在第四象限,點B在x軸正半軸上,在△OAB中,∠OAB=90°,AB=AO=6![]() ,點P為線段OA上一動點(點P不與點A和點O重合),過點P作OA的垂線交x軸于點C,以點C為正方形的一個頂點作正方形CDEF,使得點D在線段CB上,點E在線段AB上.
,點P為線段OA上一動點(點P不與點A和點O重合),過點P作OA的垂線交x軸于點C,以點C為正方形的一個頂點作正方形CDEF,使得點D在線段CB上,點E在線段AB上.
(1)①求直線AB的函數表達式.
②直接寫出直線AO的函數表達式 ;
(2)連接PF,在Rt△CPF中,∠CFP=90°時,請直接寫出點P的坐標為 ;
(3)在(2)的前提下,直線DP交y軸于點H,交CF于點K,在直線OA上存在點Q.使得△OHQ的面積與△PKE的面積相等,請直接寫出點Q的坐標 .
查看答案和解析>>
科目:初中數學 來源: 題型:
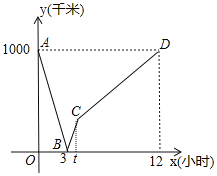
【題目】一列動車從甲地開往乙地, 一列普通列車從乙地開往甲地,兩車均勻速行駛并同時出發,設普通列車行駛的時間為![]() (小時),兩車之間的距離為
(小時),兩車之間的距離為![]() (千米),如圖中的折線表示
(千米),如圖中的折線表示![]() 與
與![]() 之間的函數關系,下列說法:①動車的速度是
之間的函數關系,下列說法:①動車的速度是![]() 千米/小時;②點B的實際意義是兩車出發后
千米/小時;②點B的實際意義是兩車出發后![]() 小時相遇;③甲、乙兩地相距
小時相遇;③甲、乙兩地相距![]() 千米;④普通列車從乙地到達甲地時間是
千米;④普通列車從乙地到達甲地時間是![]() 小時,其中不正確的有( )
小時,其中不正確的有( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,共享單車服務的推出(如圖1),極大的方便了城市公民綠色出行,圖2是某品牌某型號單車的車架新投放時的示意圖(車輪半徑約為30cm),其中BC∥直線l,∠BCE=71°,CE=54cm.
(1)求單車車座E到地面的高度;(結果精確到1cm)
(2)根據經驗,當車座E到CB的距離調整至等于人體胯高(腿長)的0.85時,坐騎比較舒適.小明的胯高為70cm,現將車座E調整至座椅舒適高度位置E′,求EE′的長.(結果精確到0.1cm)
(參考數據:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,點M是AB上的一點,點N是CB上的一點.
(1)若3BM=4CN.
①如圖1,當CN=![]() 時,判斷MN與AC的位置關系,并說明理由;
時,判斷MN與AC的位置關系,并說明理由;
②如圖2,連接AN,CM,當∠CAN與△CMB中的一個角相等時,求BM的值.
(2)當MN⊥AB時,將△NMB沿直線MN翻折得到△NMF,點B落在射線BA上的F處,設MB=x,△NMF與△ABC重疊部分的面積為y,求y關于x的函數表達式及x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】幾何模型:
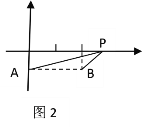
條件:如圖1,A、B是直線![]() 同旁的兩個定點.
同旁的兩個定點.

問題:在直線![]() 上確定一點P,使PA+PB的值最小.
上確定一點P,使PA+PB的值最小.
方法:作點A關于直線![]() 的對稱點A′,連接A′B交
的對稱點A′,連接A′B交![]() 于點P,則PA+PB=A′B的值最小(不必證明).
于點P,則PA+PB=A′B的值最小(不必證明).
模型應用:
(1)如圖2,已知平面直角坐標系中兩定點A(0,-1),B(2,-1),P為x軸上一動點, 則當PA+PB的值最小時,點P的橫坐標是______,此時PA+PB的最小值是______;
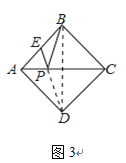
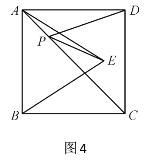
(2)如圖3,正方形ABCD的邊長為2,E為AB的中點,P是AC上一動點.由正方形對稱性可知,B與D關于直線AC對稱,連接BD,則PB+PE的最小值是______;
(3)如圖4,正方形ABCD的面積為12,△ABE是等邊三角形,點E在正方形ABCD內,在對角線AC上有一動點P,則PD+PE的最小值為 ;
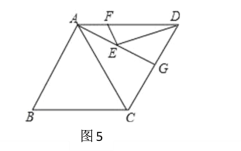
(4)如圖5,在菱形ABCD中,AB=8,∠B=60°,點G是邊CD邊的中點,點E、F分別是AG、AD上的兩個動點,則EF+ED的最小值是_______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知平行四邊形ABCD,對角線AC,BD相交于點O,∠OBC=∠OCB.
(1)求證:平行四邊形ABCD是矩形;
(2)請添加一個條件使矩形ABCD為正方形.

查看答案和解析>>
科目:初中數學 來源: 題型:
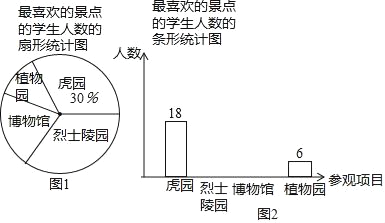
【題目】某校在一次社會實踐活動中,組織學生參觀了虎園、烈士陵園、博物館和植物園,為了解本次社會實踐活動的效果,學校隨機抽取了部分學生,對“最喜歡的景點”進行了問卷調查,并根據統計結果繪制了如下不完整的統計圖.其中最喜歡烈士陵園的學生人數與最喜歡博物館的學生人數之比為2:1,請結合統計圖解答下列問題:
(1)本次活動抽查了 名學生;
(2)請補全條形統計圖;
(3)在扇形統計圖中,最喜歡植物園的學生人數所對應扇形的圓心角是 度;
(4)該校此次參加社會實踐活動的學生有720人,請求出最喜歡烈士陵園的人數約有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com