【題目】如圖，自左至右，第1個圖由1個正六邊形、6個正方形和6個等邊三角形組成；第2個圖由2個正六邊形、11個正方形和10個等邊三角形組成；第3個圖由3個正六邊形、16個正方形和14個等邊三角形組成；…，按照此規律，第n個圖中正方形和等邊三角形的個數之和為（ ）個．
A.9nB.6nC.9n＋3D.6n+3
暑假銜接教材期末暑假預習武漢出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目：初中數學 來源： 題型：
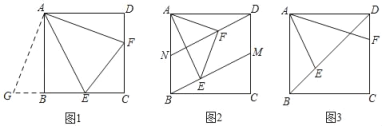
【題目】已知：正方形ABCD，∠EAF＝45°．
（1）如圖，當點E、F分別在邊BC、CD上，連接EF，求證：EF＝BE+DF；
童威同學是這樣思考的，請你和他一起完成如下解答：證明：將△ADF繞點A順時針旋轉90°，得△ABG，所以△ADF≌△ABG．
（2）如圖，點M、N分別在邊AB、CD上，且BN＝DM．當點E、F分別在BM、DN上，連接EF，探究三條線段EF、BE、DF之間滿足的數量關系，并證明你的結論．
（3）如圖，當點E、F分別在對角線BD、邊CD上．若FC＝2，則BE的長為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形ABCD中，點E、F分別在BC、CD上，△AEF是等邊三角形，連接AC交EF于點G，下列結論：①
；②AG=
GC；③BE+DF=EF；④
.其中正確的是（ ）
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y＝mx2﹣4mx+3m（m＞0）與x軸的交點為A，B，與y軸的交點為C，D為拋物線的頂點．
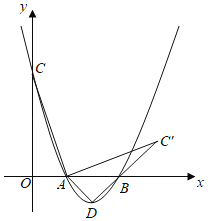
（1）直接寫出各點坐標C（ ， ），D（ ， ）；（用m表示）
（2）試說明無論m為何值，拋物線一定經過兩個定點并求出這兩個定點的坐標；
（3）①將線段AC繞點A順時針旋轉90°得到AC′，求點C′的坐標；
②連接DC'，AD，是否存在m，使得△ADC′為等腰三角形？若存在，請求出m；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中
是直徑，點
是上一點，點
是
的中點，過點作的切線，與
、
的延長線分別交于點
、
，連接
.
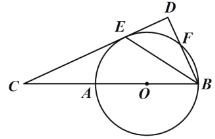
(1)求證：
.
(2)已知的半徑為2，當
為何值時，
，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（已知：如圖所示的一張矩形紙片ABCD（AD>AB），將紙片折疊一次，使點A與點C重合，再展開，折痕EF交AD邊于點E，交BC邊于點F，分別連結AF和CE．
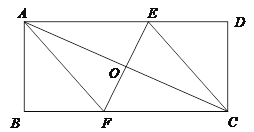
（1）求證：四邊形AFCE是菱形；
（2）若AE=10cm，△ABF的面積為24cm2，求△ABF的周長；
（3）在線段AC上是否存在一點P，使得2AE2=AC·AP？若存在，請說明點P的位置，并予以證明；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
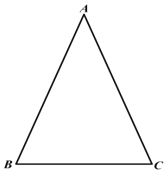
【題目】老師給同學們布置了一個“在平面內找一點，使該點到等腰三角形的三個頂點的距離相等”的尺規作圖任務：
下面是小聰同學設計的尺規作圖過程：
已知：如圖，
中，
，
求作：一點
，使得
.
作法：
①作
的平分線
交
于點
；
②作邊
的垂直平分線
，與相交于點；
③連接
，
所以，點就是所求作的點.
根據小聰同學設計的尺規作圖過程，
（1）使用直尺和圓規，補全圖形（保留作圖痕跡）
（2）完成下面的證明.
證明：∵，平分交于點，
∴
是的垂直平分線；（ ）（填推理依據）
∴
.
∵垂直平分，交于點，
∴
；（ ）（填推理依據）
∴.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小王、小張和小梅打算各自隨機選擇本周六的上午或下午去高郵湖的湖上花海去踏青郊游.
（1）小王和小張都在本周六上午去踏青郊游的概率為_______；
（2）求他們三人在同一個半天去踏青郊游的概率.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（9分）九年級數學興趣小組經過市場調查，得到某種運動服每月的銷量與售價的相關信息如下表：
售價（元/件） | 100 | 110 | 120 | 130 | … |
月銷量（件） | 200 | 180 | 160 | 140 | … |
已知該運動服的進價為每件60元，設售價為
元．
（1）請用含x的式子表示：①銷售該運動服每件的利潤是 元；②月銷量是 件；（直接寫出結果）
（2）設銷售該運動服的月利潤為
元，那么售價為多少時，當月的利潤最大，最大利潤是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
