
【題目】(綜合與實踐)如圖①,在正方形ABCD中,點E、F分別在射線CD、BC上,且BF=CE,將線段FA繞點F順時針旋轉90°得到線段FG,連接EG,試探究線段EG和BF的數量關系和位置關系.
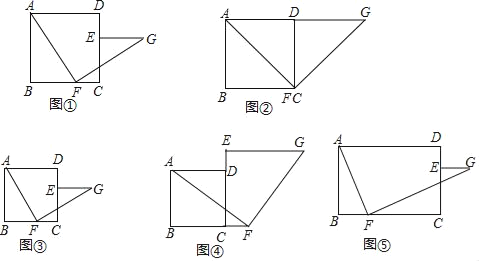
(觀察與猜想)任務一:“智慧小組”首先考慮點E、F的特殊位置如圖②,當點E與點D重合,點F與點C重合時,易知:EG與BF的數量關系是 ,EG與BF的位置關系是 .
(探究與證明)任務二:“博學小組”同學認為E、F不一定必須在特殊位置,他們分兩種情況,一種是點E、F分別在CD、BC邊上任意位置時(如圖③);一種是點E、F在CD、BC邊的延長線上的任意位置時(如圖④),線段EG與BF的數量關系與位置關系仍然成立.請你選擇其中一種情況給出證明.
(拓展與延伸)“創新小組”同學認為,若將“正方形ABCD”改為“矩形ABCD,且![]() =k(k≠1)”,點E、F分別在射線CD、BC上任意位置時,仍將線段FA繞點F順時針旋轉90°,并適當延長得到線段FG,連接EG(如圖⑤),則當線段BF、CE、AF、FG滿足一個條件 時,線段EG與BF的數量關系與位置關系仍然成立.(請你在橫線上直接寫出這個條件,無需證明)
=k(k≠1)”,點E、F分別在射線CD、BC上任意位置時,仍將線段FA繞點F順時針旋轉90°,并適當延長得到線段FG,連接EG(如圖⑤),則當線段BF、CE、AF、FG滿足一個條件 時,線段EG與BF的數量關系與位置關系仍然成立.(請你在橫線上直接寫出這個條件,無需證明)
【答案】【觀察與猜想】EG=BF,EG∥BF;【探究與證明】見解析;【拓展與延伸】![]() =
=![]() =k(k≠1).
=k(k≠1).
【解析】
【觀察與猜想】先根據SAS證明△ABC≌△GDC,得出AB=GD,∠GDC=∠B=90°,進而得出DG∥BC,△CDG是等腰直角三角形,再由等腰直角三角形的性質得出DG=CD=BC,即可得出結論;
【探究與證明】當點E、F分別在CD、BC邊上任意位置時,作GM⊥BC,交BC延長線于M,先根據AAS證明△ABF≌△FMG,得出AB=FM,BF=MG,進而可得BF=CM,而BF=CE,可得MG=CE,于是四邊形CEGM是矩形,繼而有EG=CM,EG∥CM,即可得出結論;當點E、F在CD、BC邊的延長線上的任意位置時,同上面的分析;
【拓展與延伸】作GM⊥BC,交BC延長線于M,先證明△ABF∽△FMG,得出![]() ,結合已知可得出
,結合已知可得出![]() ,
,![]() ,進而證出FM=BC,GM=CE,于是BF=CM,然后證明四邊形CEGM是矩形,進而得EG=CM,EG∥CM,即可得出結論.
,進而證出FM=BC,GM=CE,于是BF=CM,然后證明四邊形CEGM是矩形,進而得EG=CM,EG∥CM,即可得出結論.
【觀察與猜想】EG=BF,EG∥BF;
證明:如圖②,∵四邊形ABCD是正方形,
∴∠B=∠BCD=∠ADC=90°,AB=BC=CD=AD,∠ACB=∠ACD=45°,
由旋轉的性質得:GC=AC,∠ACG=90°,
∴∠ACB=∠GCD=45°,
∴△ABC≌△GDC(SAS),
∴AB=GD,∠GDC=∠B=90°,
∴DG∥BC,△CDG是等腰直角三角形,
∴DG=CD=BC,
∵點E與點D重合,點F與點C重合,
∴EG=BF,EG∥BF;
故答案為:EG=BF,EG∥BF;
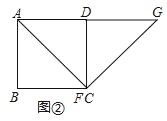
【探究與證明】證明:當點E、F分別在CD、BC邊上任意位置時,如圖③所示:
作GM⊥BC,交BC延長線于M,則∠GMF=90°,MG∥DC,
∵四邊形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,
∴∠BAF+∠BFA=90°,
由旋轉的性質得:GF=AF,∠AFG=90°,
∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,
∴△ABF≌△FMG(AAS),
∴AB=FM,BF=MG,
∵AB=BC,∴BF=CM,
∵BF=CE,∴MG=CE,
∵MG∥CE,∴四邊形CEGM是平行四邊形,
又∵∠M=90°,∴四邊形CEGM是矩形,
∴EG=CM,EG∥CM,
∴EG=BF,EG∥BF;

當點E、F在CD、BC邊的延長線上的任意位置時,如圖④所示:
作GM⊥BC,交BC延長線于M,則∠M=90°,MG∥DC,
∵四邊形ABCD是正方形,∴AB=BC,∠BCD=∠B=90°,
∴∠BAF+∠BFA=90°,
由旋轉的性質得:GF=AF,∠AFG=90°,
∴∠BFA+∠MFG=90°,∴∠BAF=∠MFG,
∴△ABF≌△FMG(AAS),
∴AB=FM,BF=MG,
∵AB=BC,∴BF=CM,
∵BF=CE,∴MG=CE,
∵MG∥CE,∴四邊形CEGM是平行四邊形,
又∵∠M=90°,∴四邊形CEGM是矩形,
∴EG=CM,EG∥CM,
∴EG=BF,EG∥BF;
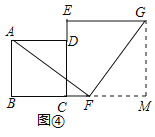
【拓展與延伸】解:![]() =k(k≠1)時,線段EG與BF的數量關系與位置關系仍然成立;理由如下:
=k(k≠1)時,線段EG與BF的數量關系與位置關系仍然成立;理由如下:
作GM⊥BC,交BC延長線于M,如圖⑤所示:則∠M=90°,MG∥DC,
∵四邊形ABCD是矩形,∴∠BCD=∠B=90°,
∴∠BAF+∠BFA=90°,∠B=∠M,
由旋轉的性質得:∠AFG=90°,∴∠BFA+∠MFG=90°,
∴∠BAF=∠MFG,∴△ABF∽△FMG,
∴![]() ,
,
∵![]() =k,∴
=k,∴![]() =k,
=k,![]() =k,
=k,
∴FM=BC,GM=CE,∴BF=CM,
∵MG∥CE,∴四邊形CEGM是平行四邊形,
又∵∠M=90°,∴四邊形CEGM是矩形,
∴EG=CM,EG∥CM,
∴EG=BF,EG∥BF;
故答案為:![]() =k(k≠1).
=k(k≠1).


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖所示是二次函數![]() 圖象的一部分,圖象過點
圖象的一部分,圖象過點![]() ,二次函數圖象對稱軸為直線
,二次函數圖象對稱軸為直線![]() ,給出五個結論:①
,給出五個結論:①![]() ;②
;②![]() ;③當
;③當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;④方程
的增大而增大;④方程![]() 的根為
的根為![]() ,
,![]() ;⑤
;⑤![]() 其中正確結論是( )
其中正確結論是( )

A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將兩塊斜邊長相等的等腰直角三角板按如圖①擺放,斜邊AB分別交CD,CE于M,N點.
(1)如果把圖①中的△BCN繞點C逆時針旋轉90°得到△ACF,連接FM,如圖②,求證:△CMF≌△CMN;
(2)將△CED繞點C旋轉,則:
①當點M,N在AB上(不與點A,B重合)時,線段AM,MN,NB之間有一個不變的關系式,請你寫出這個關系式,并說明理由;
②當點M在AB上,點N在AB的延長線上(如圖③)時,①中的關系式是否仍然成立?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象相交于
的圖象相交于![]() 、
、![]() 兩點,其中點
兩點,其中點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
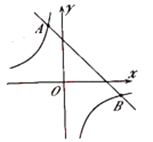
(1)根據圖象,直接寫出滿足![]() 的
的![]() 的取值范圍;
的取值范圍;
(2)求這兩個函數的表達式;
(3)點![]() 在線段
在線段![]() 上,且
上,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c交x軸分別于點A(﹣3,0),B(1,0),交y軸正半軸于點D,拋物線頂點為C.下列結論
①2a﹣b=0;
②a+b+c=0;
③當m≠﹣1時,a﹣b>am2+bm;
④當△ABC是等腰直角三角形時,a=![]() ;
;
⑤若D(0,3),則拋物線的對稱軸直線x=﹣1上的動點P與B、D兩點圍成的△PBD周長最小值為3![]() ,其中,正確的個數為( )
,其中,正確的個數為( )
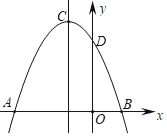
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一個二次函數滿足以下條件:
①函數圖象與x軸的交點坐標分別為A(1,0),B(x2,y2)(點B在點A的右側);
②對稱軸是x=3;
③該函數有最小值是﹣2.
(1)請根據以上信息求出二次函數表達式;
(2)將該函數圖象x>x2的部分圖象向下翻折與原圖象未翻折的部分組成圖象“G”,平行于x軸的直線與圖象“G”相交于點C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),結合畫出的函數圖象求x3+x4+x5的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一條筆直的公路上有A、B兩地,甲、乙兩輛貨車都要從A地送貨到B地,甲車先從A地出發勻速行駛,3小時后,乙車從A地出發,并沿同一路線勻速行駛,當乙車到達B地后立刻按原速返回,在返回途中第二次與甲車相遇。甲車出發的時間記為t (小時),兩車之間的距離記為y(千米),y與t的函數關系如圖所示,則乙車第二次與甲車相遇時,甲車距離A地___千米.
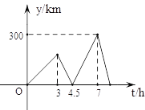
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,點E是AD邊的中點,BD,CE交于點H,BE、AH交于點G,則下列結論:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正確的是( )
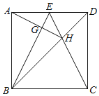
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙![]() 與菱形
與菱形![]() 在平面直角坐標系中,點
在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() 點
點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸上,且點
軸上,且點![]() 在點
在點![]() 的右側.
的右側.


(![]() )求菱形
)求菱形![]() 的周長.
的周長.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 軸向右以每秒
軸向右以每秒![]() 個單位長度的速度平移,菱形
個單位長度的速度平移,菱形![]() 沿
沿![]() 軸向左以每秒
軸向左以每秒![]() 個單位長度的速度平移,設菱形移動的時間為(
個單位長度的速度平移,設菱形移動的時間為(![]() 秒),當⊙
秒),當⊙![]() 與
與![]() 相切,且切點為
相切,且切點為![]() 的中點時,連接
的中點時,連接![]() ,求
,求![]() 的值及
的值及![]() 的度數.
的度數.
(![]() )在(
)在(![]() )的條件下,當點
)的條件下,當點![]() 與
與![]() 所在的直線的距離為
所在的直線的距離為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com