
 +
+ ,倒數差為
,倒數差為 -
- ,倒數積為
,倒數積為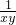 ,倒數商為
,倒數商為 ,
,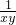 =
= ,
, +
+ =
=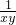 ,x=1-y,當y=1時,x=0不可取,所以y=-1,x=2;
,x=1-y,當y=1時,x=0不可取,所以y=-1,x=2; -
- =
=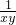 ,x=y-1,當y=1時,x=0不可取,所以y=-1,x=-2.
,x=y-1,當y=1時,x=0不可取,所以y=-1,x=-2. =1或-
=1或- .
. .
.

 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com