
【題目】如圖, 一次函數的圖象與x軸,y軸分別相交于點A,B,將△AOB沿直線AB翻折,得△ACB.若點C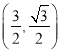 ,求該一次函數的表達式.
,求該一次函數的表達式.
【答案】y=-![]() x+
x+![]()
【解析】試題分析:求一次函數表達式,需要列兩個方程.由C點坐標,利用勾股定理可以得到AC的長,AC=OA,也就得到了,A點坐標,得到第一個方程,同時,可以得到
∠ACM=30°,所以,∠ABO=30°易得B點坐標,得到第二個方程,也就可以求出一次函數的表達式.
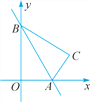
如圖,過點C作CM⊥x軸于點M,CN⊥y軸于點N.
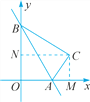
∵點C ,∴OM=NC=
,∴OM=NC=![]() ,ON=MC=
,ON=MC=![]() .
.
∵將△AOB沿直線AB翻折得到△ACB,∴OA=CA,OB=CB.
在Rt△CAM中,由勾股定理,得AC2=AM2+MC2,即OA2=(OM-OA)2+MC2,
∴OA2=![]() +
+![]() ,解得OA=1.
,解得OA=1.
∴點A(1,0).∴∠ACM=30°,∴∠ABO=30°,AB=2,∴OB=![]() ,點B(0,
,點B(0, ![]() ).
).
設直線AB的函數表達式為y=kx+b.
把點A,B的坐標代入,得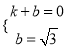 ,解得
,解得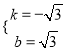
∴直線AB的函數表達式為y=-![]() x+
x+![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,AB=AC,D為邊BC上一點,以AB,BD為鄰邊作平行四邊形ABDE,連接AD,EC.
(1)求證:△ADC≌△ECD;
(2)當點D在什么位置時,四邊形ADCE是矩形,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明袋子中有1個紅球,1個綠球和n個白球,這些球除顏色外無其他差別.
(1)當n=1時,從袋中隨機摸出1個球,摸到紅球和摸到白球的可能性是否相同?
(2)從袋中隨機摸出一個球,記錄其顏色,然后放回,大量重復該實驗,發現摸到綠球的頻率穩定于0.25,則n的值是 ;
(3)當n=2時,先從袋中任意摸出1個球不放回,再從袋中任意摸出1個球,請用列表或畫樹狀圖的方法,求兩次都摸到白球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在方格紙內將△ABC水平向右平移4個單位得到△A′B′C′.
(1)補全△A′B′C′,利用網格點和直尺畫圖
(2)圖中AC與A1C1的關系是:
(3)畫出AB邊上的高線CD;
(4)畫出△ABC中AB邊上的中線CE
(5)△BCE的面積為
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,將一副直角三角板放在同一條直線AB上,其中∠ONM=30°,∠OCD=45°.
(1)將圖①中的三角板OMN沿BA的方向平移至圖②的位置,MN與CD相交于點E,求∠CEN的度數;
(2)將圖①中的三角板OMN繞點O按逆時針方向旋轉至如圖③,當∠CON=5∠DOM時,MN與CD相交于點E,請你判斷MN與BC的位置關系,并求∠CEN的度數
(3)將圖①中的三角板OMN繞點O按每秒5°的速度按逆時針方向旋轉一周,在旋轉的過程中,三角板MON運動幾秒后直線MN恰好與直線CD平行.
(4)將如圖①位置的兩塊三角板同時繞點O逆時針旋轉,速度分別每秒20°和每秒10°,當其中一個三角板回到初始位置時,兩塊三角板同時停止轉動.經過多少秒后邊OC與邊ON互相垂直.(直接寫出答案)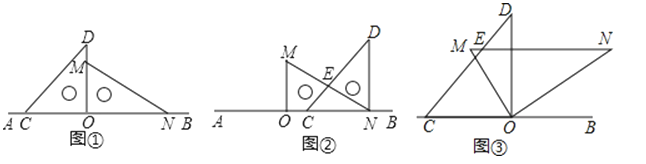
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c與x軸相交于A(﹣2,0),B(4,0),與y軸相交于點C,且拋物線經過點(2,2).
(1)求此拋物線的解析式;
(2)在拋物線的對稱軸上找一點H,使AH+CH最小,并求出點H的坐標;
(3)在第四象限內,拋物線上是否存在點M,是的以點A、B、M為頂點的三角形與△ABC相似?若存在,請求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們運用圖(Ⅰ)中大正方形的面積可表示為(a+b)2 , 也可表示為c3+4(![]() ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4(![]() ab)由此推導出一個重要的結論a2+b2=c2 , 這個重要的結論就是著名的“勾股定理”.這種根據圖形可以極簡單地直觀推論或驗證數學規律和公式的方法,簡稱“無字證明”.
ab)由此推導出一個重要的結論a2+b2=c2 , 這個重要的結論就是著名的“勾股定理”.這種根據圖形可以極簡單地直觀推論或驗證數學規律和公式的方法,簡稱“無字證明”.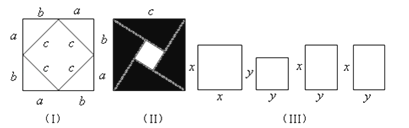
(1)請你用圖(Ⅱ)(2002年國際數學家大會會標)的面積表達式驗證勾股定理(其中四個直角三角形的較大的直角邊長都為a,較小的直角邊長都為b,斜邊長都為c).
(2)請你用(Ⅲ)提供的圖形進行組合,用組合圖形的面積表達式驗證:(x+2y)2=x2+4xy+4y2 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在正方形ABCD中,P是對角線AC上的一點,點E在BC的延長線上,且PE=PB.

(1)求證:△BCP≌△DCP;
(2)求證:∠DPE=∠ABC;
(3)把正方形ABCD改為菱形,其它條件不變(如圖②),若∠ABC=58°,則∠DPE= 度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com