【題目】如圖，已知直線
分別交x軸、y軸于A、B兩點，拋物線
經過A、B兩點，點C是拋物線與x軸的另一個交點（與A點不重合）．
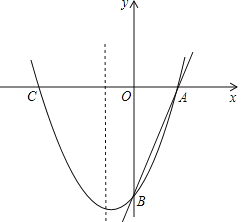
（1）求拋物線的解析式；
（2）求△ABC的面積；
（3）在拋物線的對稱軸上，是否存在點M，使△ABM為等腰三角形？若不存在，請說明理由；若存在，求出點M的坐標．
【答案】（1）
；（2）6；（3）M1（﹣1，
），M2（﹣1，
），M3（﹣1，0），M4（﹣1，﹣1）
【解析】試題分析：（1）由直線解析式求出點A及點B的坐標，將點A及點B的坐標代入拋物線解析式，可得出b、c的值，即可求出拋物線解析式；
（2）由（1）求得的拋物線解析式，求出點C的坐標，從而求出AC的長度，代入三角形的面積公式即可計算；
（3）根據點M在拋物線對稱軸上，可設點M的坐標為（﹣1，m），分三種情況討論，①MA=BA，②MB=BA，③MB=MA，列方程，求出m的值后即可．
試題解析：（1）∵直線
分別交x軸、y軸于A、B兩點，∴可得A（1，0），B（0，﹣3），把A、B兩點的坐標分別代入
得：
，解得：
，∴拋物線解析式為：；
（2）令y=0得：
，解得：
，
，則C點坐標為：（﹣3，0），AC=4，故可得S△ABC=
AC×OB=×4×3=6；
（3）存在，理由如下：拋物線的對稱軸為：x=﹣1，假設存在M（﹣1，m）滿足題意：分三種情況討論：
①當MA=AB時，∵OA=1，OB=3，∴AB=
，
，解得：m=
，∴M1（﹣1，），M2（﹣1，）；
②當MB=BA時，
，解得：M3=0，M4=﹣6，∴M3（﹣1，0），M4（﹣1，﹣6）（不合題意舍去）；
③當MB=MA時，
，解得：m=﹣1，∴M5（﹣1，﹣1），答：共存在4個點M1（﹣1，），M2（﹣1，），M3（﹣1，0），M4（﹣1，﹣1）使△ABM為等腰三角形．
科目：初中數學 來源： 題型：
【題目】如圖，AB∥FC，D是AB上一點，DF交AC于點E，DE=FE，分別延長FD和CB交于點G．
（1）求證：△ADE≌△CFE；
（2）若GB=2，BC=4，BD=1，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某花店準備購進甲、乙兩種花卉，若購進甲種花卉20盆，乙種花卉50盆，需要720元；若購進甲種花卉40盆，乙種花卉30盆，需要880元．
（1）求購進甲、乙兩種花卉，每盆各需多少元？
（2）該花店銷售甲種花卉每盆可獲利6元，銷售乙種花卉每盆可獲利1元，現該花店準備拿出800元全部用來購進這兩種花卉，設購進甲種花卉x盆，全部銷售后獲得的利潤為W元，求W與x之間的函數關系式；
（3）在（2）的條件下，考慮到顧客需求，要求購進乙種花卉的數量不少于甲種花卉數量的6倍，且不超過甲種花卉數量的8倍，那么該花店共有幾種購進方案？在所有的購進方案中，哪種方案獲利最大？最大利潤是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在數軸上點A表示的數為a，點B表示的數為b，且a，b滿足|a+2|+（3a+b）2=0，O為原點．
（1）則a= ，b= ；
（2）若動點P從點A出發，以每秒1個單位長度的速度沿數軸向右勻速運動，
①當PO=2PB時，求點P的運動時間t；
②當點P運動到線段OB上時，分別取AP和OB的中點E、F，則
的值為 ．
（3）有一動點Q從原點O出發第一次向左運動1個單位長度，然后在新的位置第二次運動，向右運動2個單位長度，在此位置第三次運動，向左運動3個單位長度…按照如此規律不斷地左右運動，當運動到2015次時，求點Q所對應的有理數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠AOB是平角，OD是∠AOC的角平分線，∠COE＝∠BOE．
（1）若∠AOC＝ 50°，則∠DOE＝ °；
（2）當∠AOC的大小發生改變時，∠DOE的大小是否發生改變？為什么？
（3）圖中與∠COD互補角的個數隨∠AOC的度數變化而變化，直接寫出與∠COD互補的角的個數及對應的∠AOC的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知忠華家、桂枝家、文興家及學校在一條南北向的大街旁．一天，放學后他們三人從學校出發，先向南走250米達到桂枝家（記為點A），然后再向南走250米到文興家（記為點B），從文興家向北走1000米到達忠華家（記為點C）．
（1）以學校為原點，以向北方向為正方向，用1個單位長度表示實際距離250米畫出一條數軸，在數軸上用字母表示出忠華家、桂枝家、文興家的位置．
（2）忠華家在學校的哪個方向，到學校的距離是多少米？
（3）如果以向南方向為正方向建立數軸，對確定忠華家相對于學校的位置有影響嗎？說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某服裝店專營一批進價為每件200元的品牌襯衫，每件售價為300元時，每天可售出40件，若每件降價10元，則第天多售出10件，請根據以上信息解答下列問題：
（1）為了使銷售該品牌襯衫每天獲利4500元，并且讓利于顧客，每件售價應為多少元；
（2）該服裝店將該品牌的襯衫銷售完，在補貨時廠家只剩100件，經協商每件降價a元，全部拿回。按（1）中的價格售出80件后，剩余的按八折銷售。售完這100件襯衫獲利20%，求a的值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，貨輪甲從港口O出發，沿東偏南
的方向航行20海里后到達A處．（已知四個圓圈的半徑（由小到大）分別是5海里，10海里，15海里，20海里．）
（1）寫出在港口O觀測燈塔B，C的方向及它們與港口的距離；
（2）已知燈塔D在港口O的南偏西
方向上，且與燈塔B相距35海里，在圖中標出燈塔D的位置．
（3）貨輪乙從港口O出發，沿正東方向航行15海里到達P處后，需把航行方向調整到與貨輪甲的航行方向一致，此時貨輪乙應向左（或右）轉多少度？并畫出貨輪乙航行線路示意圖．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
