
【題目】已知:正方形ABCD中,∠MAN=45°,∠MAN繞點A順時針旋轉,它的兩邊分別交CB、DC(或它們的延長線)于點M、N.當∠MAN繞點A旋轉到BM=DN時(如圖1),易證BM+DN=MN.
(1)當∠MAN繞點A旋轉到BM≠DN時(如圖2),線段BM、DN和MN之間有怎樣的數量關系?寫出猜想,并加以證明;
(2)當∠MAN繞點A旋轉到如圖3的位置時,線段BM、DN和MN之間又有怎樣的數量關系?請直接寫出你的猜想.
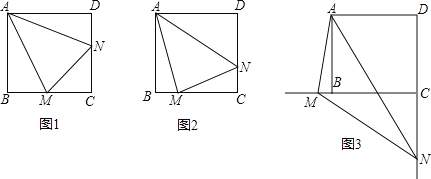
【答案】(1)DN+BM=MN;(2)DN﹣BM=MN.
【解析】
試題分析:(1)BM+DN=MN成立,證得B、E、M三點共線即可得到△AEM≌△ANM,從而證得ME=MN.
(2)DN﹣BM=MN.證明方法與(1)類似.
解:(1)BM+DN=MN成立.
證明:如圖,把△ADN繞點A順時針旋轉90°,

得到△ABE,則可證得E、B、M三點共線(圖形畫正確).
∴∠EAM=90°﹣∠NAM=90°﹣45°=45°,
又∵∠NAM=45°,
∴在△AEM與△ANM中,
∴△AEM≌△ANM(SAS),
∴ME=MN,
∵ME=BE+BM=DN+BM,
∴DN+BM=MN;
(2)DN﹣BM=MN.
在線段DN上截取DQ=BM,
在△ADQ與△ABM中,
∵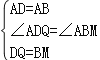 ,
,
∴△ADQ≌△ABM(SAS),
∴∠DAQ=∠BAM,
∴∠QAN=∠MAN.
在△AMN和△AQN中,

∴△AMN≌△AQN(SAS),
∴MN=QN,
∴DN﹣BM=MN.



科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=x+3分別交x軸、y軸于A,C兩點,拋物線y=ax2+bx+c(a≠0),經過A,C兩點,與x軸交于點B(1,0).
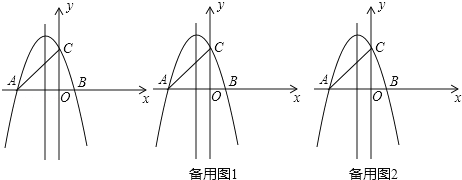
(1)求拋物線的解析式;
(2)點D為直線AC上一點,點E為拋物線上一點,且D,E兩點的橫坐標都為2,點F為x軸上的點,若四邊形ADEF是平行四邊形,請直接寫出點F的坐標;
(3)若點P是線段AC上的一個動點,過點P作x軸的垂線,交拋物線于點Q,連接AQ,CQ,求△ACQ的面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列運算正確的是( )
A. (﹣3)+(﹣4)=3+(﹣4)= ﹣1
B. (﹣3)+(﹣4)=﹣3+4=1
C. (﹣3)﹣(﹣4)=﹣3+4=1
D. (﹣3)﹣(﹣4)=﹣3﹣4=﹣7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是△ABC的兩外角平分線的交點,下列結論:①OB=OC;②點O到AB、AC的距離相等;③點O到△ABC的三邊的距離相等;④點O在∠A的平分線上.其中結論正確的個數是( )
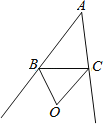
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有2012個數排成一行,其中任意相鄰的三個數中,中間的數等于它前后兩數的和,若第一個數和第二個數都是1,則這2012個數的和等于 ( )
A.-1 B. 0 C. 2 D. 2010
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com