
【題目】如圖,已知拋物線y=﹣![]() x2+bx+c與坐標軸分別交于點A(0,8)、B(8,0)和點E,動點C從原點O開始沿OA方向以每秒1個單位長度移動,動點D從點B開始沿BO方向以每秒1個單位長度移動,動點C、D同時出發,當動點D到達原點O時,點C、D停止運動.
x2+bx+c與坐標軸分別交于點A(0,8)、B(8,0)和點E,動點C從原點O開始沿OA方向以每秒1個單位長度移動,動點D從點B開始沿BO方向以每秒1個單位長度移動,動點C、D同時出發,當動點D到達原點O時,點C、D停止運動.

(1)直接寫出拋物線的解析式: ;
(2)求△CED的面積S與D點運動時間t的函數解析式;當t為何值時,△CED的面積最大?最大面積是多少?
(3)當△CED的面積最大時,在拋物線上是否存在點P(點E除外),使△PCD的面積等于△CED的最大面積?若存在,求出P點的坐標;若不存在,請說明理由.
【答案】(1)y=﹣![]() x2+3x+8;(2)當t=5時,S最大=
x2+3x+8;(2)當t=5時,S最大=![]() ;(3)當△CED的面積最大時,在拋物線上存在點P(點E除外),使△PCD的面積等于△CED的最大面積,點P的坐標為:P(
;(3)當△CED的面積最大時,在拋物線上存在點P(點E除外),使△PCD的面積等于△CED的最大面積,點P的坐標為:P(![]() ,﹣
,﹣![]() )或P(8,0)或P(
)或P(8,0)或P(![]() ,
,![]() ).
).
【解析】
試題分析:(1)將點A(0,8)、B(8,0)代入拋物線y=﹣![]() x2+bx+c即可求出拋物線的解析式為:y=﹣
x2+bx+c即可求出拋物線的解析式為:y=﹣![]() x2+3x+8;
x2+3x+8;
(2)根據題意得:當D點運動t秒時,BD=t,OC=t,然后由點A(0,8)、B(8,0),可得OA=8,OB=8,從而可得OD=8﹣t,然后令y=0,求出點E的坐標為(﹣2,0),進而可得OE=2,DE=2+8﹣t=10﹣t,然后利用三角形的面積公式即可求△CED的面積S與D點運動時間t的函數解析式為:S=﹣![]() t2+5t,然后轉化為頂點式即可求出最值為:S最大=
t2+5t,然后轉化為頂點式即可求出最值為:S最大=![]() ;
;
(3)由(2)知:當t=5時,S最大=![]() ,進而可知:當t=5時,OC=5,OD=3,進而可得CD=
,進而可知:當t=5時,OC=5,OD=3,進而可得CD=![]() ,從而確定C(0,5),D(3,0)然后根據待定系數法求出直線CD的解析式為:y=﹣
,從而確定C(0,5),D(3,0)然后根據待定系數法求出直線CD的解析式為:y=﹣![]() x+5,然后過E點作EF∥CD,交拋物線與點P,然后求出直線EF的解析式,與拋物線聯立方程組解得即可得到其中的一個點P的坐標,然后利用面積法求出點E到CD的距離為:
x+5,然后過E點作EF∥CD,交拋物線與點P,然后求出直線EF的解析式,與拋物線聯立方程組解得即可得到其中的一個點P的坐標,然后利用面積法求出點E到CD的距離為:![]() ,然后過點D作DN⊥CD,垂足為N,且使DN=
,然后過點D作DN⊥CD,垂足為N,且使DN=![]() ,然后求出N的坐標,然后過點N作NH∥CD,與拋物線交與點P,然后求出直線NH的解析式,與拋物線聯立方程組求解即可得到其中的另兩個點P的坐標.
,然后求出N的坐標,然后過點N作NH∥CD,與拋物線交與點P,然后求出直線NH的解析式,與拋物線聯立方程組求解即可得到其中的另兩個點P的坐標.
解:(1)將點A(0,8)、B(8,0)代入拋物線y=﹣![]() x2+bx+c得:
x2+bx+c得: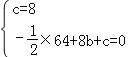 ,
,
解得:b=3,c=8,
∴拋物線的解析式為:y=﹣![]() x2+3x+8,
x2+3x+8,
故答案為:y=﹣![]() x2+3x+8;
x2+3x+8;
(2)∵點A(0,8)、B(8,0),
∴OA=8,OB=8,
令y=0,得:﹣![]() x2+3x+8=0,
x2+3x+8=0,
解得:x18,x2=2,
∵點E在x軸的負半軸上,
∴點E(﹣2,0),
∴OE=2,
根據題意得:當D點運動t秒時,BD=t,OC=t,
∴OD=8﹣t,
∴DE=OE+OD=10﹣t,
∴S=![]() DEOC=
DEOC=![]() (10﹣t)t=﹣
(10﹣t)t=﹣![]() t2+5t,
t2+5t,
即S=﹣![]() t2+5t=﹣
t2+5t=﹣![]() (t﹣5)2+
(t﹣5)2+![]() ,
,
∴當t=5時,S最大=![]() ;
;
(3)由(2)知:當t=5時,S最大=![]() ,
,
∴當t=5時,OC=5,OD=3,
∴C(0,5),D(3,0),
由勾股定理得:CD=![]() ,
,
設直線CD的解析式為:y=kx+b,
將C(0,5),D(3,0),代入上式得:
k=﹣![]() ,b=5,
,b=5,
∴直線CD的解析式為:y=﹣![]() x+5,
x+5,
過E點作EF∥CD,交拋物線與點P,如圖1,
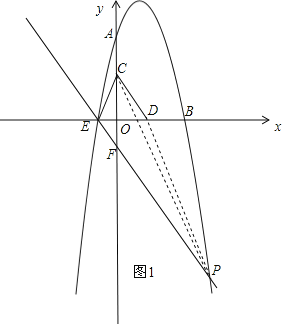
設直線EF的解析式為:y=﹣![]() x+b,
x+b,
將E(﹣2,0)代入得:b=﹣![]() ,
,
∴直線EF的解析式為:y=﹣![]() x﹣
x﹣![]() ,
,
將y=﹣![]() x﹣
x﹣![]() ,與y=﹣
,與y=﹣![]() x2+3x+8聯立成方程組得:
x2+3x+8聯立成方程組得:
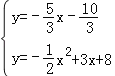 ,
,
解得: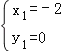 ,
,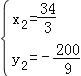 ,
,
∴P(![]() ,﹣
,﹣![]() );
);
過點E作EG⊥CD,垂足為G,
∵當t=5時,S△ECD=![]() =
=![]() ,
,
∴EG=![]() ,
,
過點D作DN⊥CD,垂足為N,且使DN=![]() ,過點N作NM⊥x軸,垂足為M,如圖2,
,過點N作NM⊥x軸,垂足為M,如圖2,
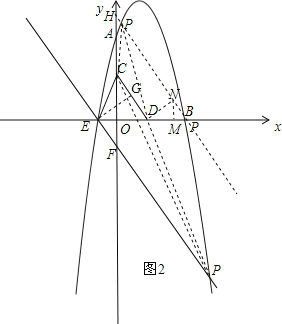
可得△EGD∽△DMN,
∴![]() ,
,
即: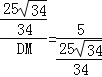 ,
,
解得:DM=![]() ,
,
∴OM=![]() ,
,
由勾股定理得:MN=![]() =
=![]() ,
,
∴N(![]() ,
,![]() ),
),
過點N作NH∥CD,與拋物線交與點P,如圖2,
設直線NH的解析式為:y=﹣![]() x+b,
x+b,
將N(![]() ,
,![]() ),代入上式得:b=
),代入上式得:b=![]() ,
,
∴直線NH的解析式為:y=﹣![]() x+
x+![]() ,
,
將y=﹣![]() x+
x+![]() ,與y=﹣
,與y=﹣![]() x2+3x+8聯立成方程組得:
x2+3x+8聯立成方程組得:
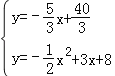 ,
,
解得:![]() ,
,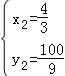 ,
,
∴P(8,0)或P(![]() ,
,![]() ),
),
綜上所述:當△CED的面積最大時,在拋物線上存在點P(點E除外),使△PCD的面積等于△CED的最大面積,點P的坐標為:P(![]() ,﹣
,﹣![]() )或P(8,0)或P(
)或P(8,0)或P(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】在一個口袋里有四個完全相同的小球,把它們分別標號為1,2,3,4,小明和小強采取的摸取方法分別是:
小明:隨機摸取一個小球記下標號,然后放回,再隨機摸取一個小球,記下標號;
小強:隨機摸取一個小球記下標號,不放回,再隨機摸取一個小球,記下標號.
(1)用畫樹狀圖(或列表法)分別表示小明和小強摸球的所有可能出現的結果;
(2)分別求出小明和小強兩次摸球的標號之和等于5的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】君暢中學計劃購買一些文具送給學生,為此學校決定圍繞“在筆袋、圓規、直尺、鋼筆四種文具中,你最需要的文具是什么?(必選且只選一種)”的問題,在全校范圍內隨機抽取部分學生進行問卷調查,將調查結果整理后繪制成如圖所示的不完整的統計圖,請你根據以上信息回答下列問題:
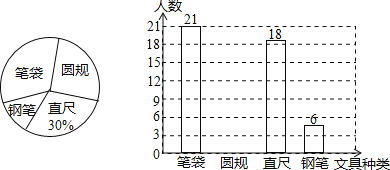
(1)在這次調查中,最需要圓規的學生有多少名?并補全條形統計圖;
(2)如果全校有970名學生,請你估計全校學生中最需要鋼筆的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面圖形上的任意兩點P,Q,如果經過某種變換得到新圖形上的對應點P′,Q′,保持PQ=P′Q′,我們把這種變換稱為“等距變換”,下列變換中不一定是等距變換的是( )
A.平移 B.旋轉 C.軸對稱 D.位似
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一副三角尺ABC與BDE按如圖所示那樣拼在一起,其中A、B、D三點在同一直線上,BM為∠CBE的平分線,BN為∠DBE的平分線,則∠MBN的度數是( )
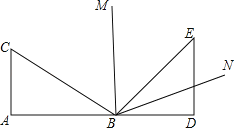
A.60° B.67.5° C.75° D.85°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=90°,OA=9cm,OB=3cm,一機器人在點B處看見一個小球從點A出發沿著AO方向勻速滾向點O,機器人立即從點B出發,沿BC方向勻速前進攔截小球,恰好在點C處截住了小球.如果小球滾動的速度與機器人行走的速度相等,那么機器人行走的路程BC是多少?
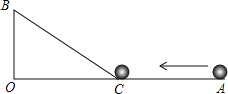
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列結論正確的是( )
A.0是正數也是有理數
B.兩數之積為正,這兩數同為正
C.幾個數相乘,積的符號由負因數的個數決定
D.互為相反數的兩個數的絕對值相等.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com