科目：初中數學 來源： 題型：
若m為不等于零的實數，則關于x的方程x2+mx﹣m2=0的根的情況是（ ）
A．有兩個相等的實數根 B．有兩個不等的實數根
C．有兩個實數根 D．無實數根
查看答案和解析>>
科目：初中數學 來源： 題型：
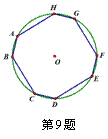
如圖，已知在⊙O中，AB=CD=EF=HG，BC=DE=FG=AH，則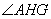
的度數是（ ）
A.、120° B.、125° C.、130° D.、135°
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
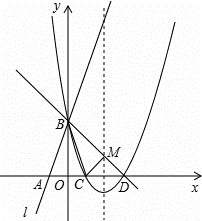
如圖所示，直線l：y=3x+3與x軸交于點A，與y軸交于點B．把△AOB沿y軸翻折，點A落到點C，拋物線過點B、C和D（3，0）．
（1）求直線BD和拋物線的解析式．
（2）若BD與拋物線的對稱軸交于點M，點N在坐標軸上，以點N、B、D為頂點的三角形與△MCD相似，求所有滿足條件的點N的坐標．
（3）在拋物線上是否存在點P，使S△PBD=6？若存在，求出點P的坐標；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
勾股定理是一條古老的數學定理，它有很多種證明方法，我國漢代數學家趙爽根據弦圖，利用面積法進行證明，著名數學家華羅庚曾提出把“數形關系”(勾股定理)帶到其他星球，作為地球人與其他星球“人”進行第一次“談話”的語言．
[定理表述]
請你根據圖1中的直角三角形敘述勾股定理(用文字及符號語言敘述)．
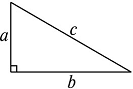
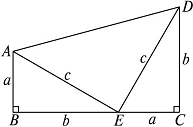
圖1 圖2
[嘗試證明]
以圖1中的直角三角形為基礎，可以構造出以a，b為底，以a＋b為高的直角梯形(如圖2)，請你利用圖2，驗證勾股定理．
[知識拓展]
利用圖2中的直角梯形，我們可以證明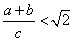
.其證明步驟如下：
∵BC＝a＋b，AD＝__________，
又∵在直角梯形ABCD中有BC__________AD(填大小關系)，即__________，
∴.
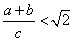查看答案和解析>>
科目：初中數學 來源： 題型：
下列語句是命題的是( )．
A．延長線段AB到C點
B．同一平面內兩條直線被第三條直線所截，同旁內角
互補
C．今天你上網了嗎？
D．求五邊形的內角和
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
）在反比例函數圖象上，則此反比例函數圖象的解析式是 .
經過點A（-2，n），則n的值為（ ）
B、
C、
D、
， MN=2，求圓心O到AB的距離。