已知一組數據x1,x2,x3,x4,x5的平均數是2,方差是3,那么另一組數據2x1-1,2x2-1,2x3-1,2x4-1,2x5-1的平均數是 ,方差是 .
【答案】
分析:根據平均數公式與方差公式即可求解.
解答:解:∵x
1,x
2,x
3,x
4,x
5的平均數是2,
∴

( x
1+x
2+x
3+x
4+x
5)=2,
∴2x
1-1,2x
2-1,2x
3-1,2x
4-1,2x
5-1,的平均數是

[(2x
1-1)+(2x
2-1)+(2x
3-1)+(2x
4-1)+(2x
5-1)],
=2×

( x
1+x
2+x
3+x
4+x
5)-1=3.
∵數據x
1,x
2,x
3,x
4,x
5的平均數是2,方差是3,
∴

[(x
1-2)
2+(x
2-2)
2+[(x
3-2)
2+(x
4-2)
2+(x
5-2)
2]=3①;
方差=

[(2x
1-1-3)
2+(2x
2-1-3)
2+(2x
3-1-3)
2+(2x
4-1-3)
2+(2x
5-1-3)
2]
=

[4(x
1-2)
2+4(x
2-2)
2+4(x
3-2)
2+4(x
4-2)
2+4(x
5-2)
2]
=

×4[(x
1-2)
2+(x
2-2)
2+(x
3-2)
2+(x
4-2)
2+(x
5-2)
2]②
把①代入②得,方差是:3×4=12.
故答案為:3;12.
點評:本題考查了平均數的計算公式和方差的定義:一般地設n個數據,x
1,x
2,…x
n的平均數為
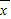
,則方差S
2=
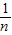
[(x
1-
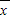
)
2+(x
2-
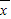
)
2+…+(x
n-
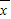
)
2],它反映了一組數據的波動大小,方差越大,波動性越大,反之也成立.

 ( x1+x2+x3+x4+x5)=2,
( x1+x2+x3+x4+x5)=2, [(2x1-1)+(2x2-1)+(2x3-1)+(2x4-1)+(2x5-1)],
[(2x1-1)+(2x2-1)+(2x3-1)+(2x4-1)+(2x5-1)], ( x1+x2+x3+x4+x5)-1=3.
( x1+x2+x3+x4+x5)-1=3. [(x1-2)2+(x2-2)2+[(x3-2)2+(x4-2)2+(x5-2)2]=3①;
[(x1-2)2+(x2-2)2+[(x3-2)2+(x4-2)2+(x5-2)2]=3①; [(2x1-1-3)2+(2x2-1-3)2+(2x3-1-3)2+(2x4-1-3)2+(2x5-1-3)2]
[(2x1-1-3)2+(2x2-1-3)2+(2x3-1-3)2+(2x4-1-3)2+(2x5-1-3)2] [4(x1-2)2+4(x2-2)2+4(x3-2)2+4(x4-2)2+4(x5-2)2]
[4(x1-2)2+4(x2-2)2+4(x3-2)2+4(x4-2)2+4(x5-2)2] ×4[(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2+(x5-2)2]②
×4[(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2+(x5-2)2]②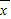 ,則方差S2=
,則方差S2=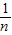 [(x1-
[(x1-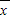 )2+(x2-
)2+(x2-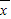 )2+…+(xn-
)2+…+(xn-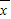 )2],它反映了一組數據的波動大小,方差越大,波動性越大,反之也成立.
)2],它反映了一組數據的波動大小,方差越大,波動性越大,反之也成立. 

 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案