
如圖所示⊙O的直徑DF與弦AB交于點E,C為⊙O外一點,CB⊥AB,G是直線CD上一點,∠ADG=∠ABD,求證:AD·CE=DE·DF.
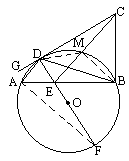
(說明:(1)如果你經歷反復探索,沒有找到解決問題地方法,請你把探索過程中的某種思維推導過程寫出來,(要求至少寫3步).(2)在你歷經說明(1)的過程之后,可以從下列①、②、③中選取一個補充或更換已知條件,完成你的證明.)
①∠CDB=∠CEB;②AD∥EC;③∠DEC=∠ADF,且∠CDE=90“
|
名師導引:關鍵是證∠ABD=∠DCE,連AF證∠DCE=∠DBE是難點,∵Rt△CDE與Rt△CBE有公共斜邊,∴有公共外接圓. 解答:如圖,連結AF,則∠ABD=∠F,而∠ADG=∠ABD,∴∠ADG=∠F,又∵DF為⊙O直徑,∴∠DAF= (一)寫出探索過程: 如圖;連接AF.∵DF為⊙O直徑,∴∠DAF= (二)選取①證明,如圖,連接AF,則∠ABD=∠F.
∵∠ADG=∠ABD,∴∠ADG=∠F,又∵DF是⊙O直徑,∴∠DAF= (三)選取②,如圖連接AF,得∠DAF=∠CDE= |


科目:初中數學 來源: 題型:
(本題滿分11分)
如圖所示,⊙![]() 的直徑
的直徑![]() ,
,![]() 和
和![]() 是它的兩條切線,
是它的兩條切線,![]() 為射線
為射線![]() 上的動點(不與
上的動點(不與![]() 重合),
重合),![]() 切⊙
切⊙![]() 于
于![]() ,交
,交![]() 于
于![]() ,設
,設![]() .
.

(1)求![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)若⊙![]() 與⊙
與⊙![]() 外切,且⊙
外切,且⊙![]() 分別與
分別與![]()
相切于點![]() ,求
,求![]() 為何值時⊙
為何值時⊙![]() 半徑為1.
半徑為1.
查看答案和解析>>
科目:初中數學 來源: 題型:
 的直徑
的直徑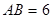 ,
, 和
和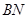 是它的兩條切線,
是它的兩條切線,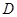 為射線
為射線 上的動點(不與
上的動點(不與 重合),
重合), 切⊙
切⊙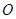 于
于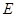 ,交
,交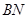 于
于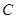 ,設
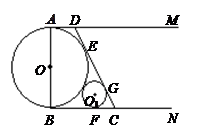
,設 .
.
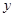 與
與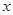 的函數關系式;
的函數關系式;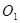 與⊙
與⊙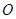 外切,且⊙
外切,且⊙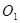 分別與
分別與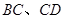
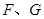 ,求
,求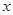 為何值時⊙
為何值時⊙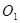 半徑為1.
半徑為1.查看答案和解析>>
科目:初中數學 來源:2012屆廣西省貴港市九年級第一次教學質量監測數學卷 題型:解答題
(本題滿分11分)
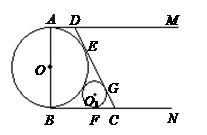
如圖所示,⊙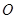 的直徑
的直徑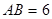 ,
,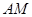 和
和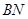 是它的兩條切線,
是它的兩條切線,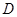 為射線
為射線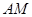 上的動點(不與
上的動點(不與 重合),
重合),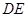 切⊙
切⊙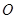 于
于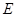 ,交
,交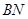 于
于 ,設
,設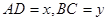 .
.
(1)求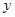 與
與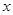 的函數關系式;
的函數關系式;
(2)若⊙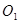 與⊙
與⊙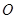 外切,且⊙
外切,且⊙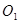 分別與
分別與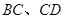
相切于點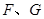 ,求
,求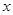 為何值時⊙
為何值時⊙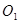 半徑為1.
半徑為1.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年廣西省貴港市九年級第一次教學質量監測數學卷 題型:解答題
(本題滿分11分)
如圖所示,⊙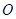 的直徑
的直徑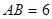 ,
,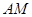 和
和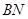 是它的兩條切線,
是它的兩條切線,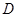 為射線
為射線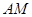 上的動點(不與
上的動點(不與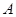 重合),
重合),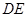 切⊙
切⊙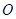 于
于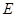 ,交
,交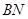 于
于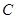 ,設
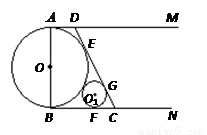
,設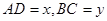 .
.
(1)求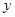 與
與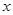 的函數關系式;
的函數關系式;
(2)若⊙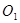 與⊙
與⊙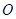 外切,且⊙
外切,且⊙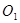 分別與
分別與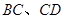
相切于點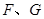 ,求
,求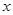 為何值時⊙
為何值時⊙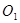 半徑為1.
半徑為1.
查看答案和解析>>
科目:初中數學 來源: 題型:
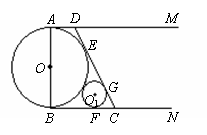
如圖所示,⊙![]() 的直徑
的直徑![]() ,
,![]() 和
和![]() 是它的兩條切線,
是它的兩條切線,![]() 為射線
為射線![]() 上的動點(不與
上的動點(不與![]() 重合),
重合),![]() 切⊙
切⊙![]() 于
于![]() ,交
,交![]() 于
于![]() ,設
,設![]() .
.
(1)求![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)若⊙![]() 與⊙
與⊙![]() 外切,且⊙
外切,且⊙![]() 分別與
分別與![]()
相切于點![]() ,求
,求![]() 為何值時⊙
為何值時⊙![]() 半徑為1.
半徑為1.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com