
 x2上的三點,A1B1、A2B2、A3B3分別垂直于x軸,垂足為B1、B2、B3,直線A2B2交線段A1A3于點C.
x2上的三點,A1B1、A2B2、A3B3分別垂直于x軸,垂足為B1、B2、B3,直線A2B2交線段A1A3于點C. x2改為拋物線y=
x2改為拋物線y= x2-x+1,A1、A2、A3三點的橫坐標為連續整數,其他條件不變,求線段CA2的長;
x2-x+1,A1、A2、A3三點的橫坐標為連續整數,其他條件不變,求線段CA2的長; x2改為拋物線y=ax2+bx+c,A1、A2、A3三點的橫坐標為連續整數,其他條件不變,請猜想線段CA2的長(用a、b、c表示,并直接寫出答案).
x2改為拋物線y=ax2+bx+c,A1、A2、A3三點的橫坐標為連續整數,其他條件不變,請猜想線段CA2的長(用a、b、c表示,并直接寫出答案).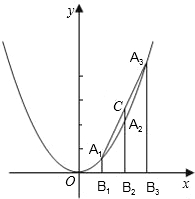
 ×12=
×12= ,A2B2=
,A2B2= ×22=2,A3B3=
×22=2,A3B3= ×32=
×32=


 ,
, =
=
 -2=
-2= .
. ×12=
×12= ,A2B2=
,A2B2= ×22=2,A3B3=
×22=2,A3B3= ×32=
×32=
 (A1B1+A3B3)=
(A1B1+A3B3)= (
( +
+ )=
)=
 -2=
-2= .
. (n-1)2-(n-1)+1,
(n-1)2-(n-1)+1, n2-n+1,
n2-n+1, (n+1)2-(n+1)+1
(n+1)2-(n+1)+1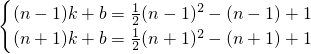
 ,
, n2+
n2+ .
. n2+
n2+ =
= n2-n+
n2-n+
 n2-n+
n2-n+ -
- n2+n-1=
n2+n-1=
 (n-1)2-(n-1)+1,
(n-1)2-(n-1)+1, n2-n+1,
n2-n+1, (n+1)2-(n+1)+1
(n+1)2-(n+1)+1 (A1B1+A3B3)
(A1B1+A3B3) [
[ (n-1)2-(n-1)+1+
(n-1)2-(n-1)+1+ (n+1)2-(n+1)+1]
(n+1)2-(n+1)+1] n2-n+
n2-n+
 n2-n+
n2-n+ -(
-( n2-n+1)=
n2-n+1)= .
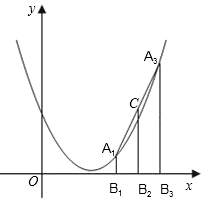
. x2上的三點,A1、A2、A3三點的橫坐標依次為1,2,3,代入函數解析式就可以求出三個點的坐標,再根據待定系數法就可以求出直線A1A3的解析式.求出直線B2A2與A1A3的交點坐標,進而求出A2C的長.
x2上的三點,A1、A2、A3三點的橫坐標依次為1,2,3,代入函數解析式就可以求出三個點的坐標,再根據待定系數法就可以求出直線A1A3的解析式.求出直線B2A2與A1A3的交點坐標,進而求出A2C的長.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| 1 | 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知A1,A2,A3,…,A2006是x軸上的點,且OA1=A1A2=A2A3=…=A2005A2006=1,分別過點A1,A2,A3,…,A2006作x軸的垂線交二次函數y=x2(x≥0)的圖象于點P1,P2,P3,…,P2006點,若記△OA1P1的面積為S1,過點P1作P1B1⊥A2P2于點B1,記△P1B1P2的面積為S2,過點P2作P2B2⊥A3P3于點B2,記△P2B2P3的面積為S3,…,依次進行下去,最后記△P2005B2005P2006的面積為S2006,則S2006-S2005=
如圖,已知A1,A2,A3,…,A2006是x軸上的點,且OA1=A1A2=A2A3=…=A2005A2006=1,分別過點A1,A2,A3,…,A2006作x軸的垂線交二次函數y=x2(x≥0)的圖象于點P1,P2,P3,…,P2006點,若記△OA1P1的面積為S1,過點P1作P1B1⊥A2P2于點B1,記△P1B1P2的面積為S2,過點P2作P2B2⊥A3P3于點B2,記△P2B2P3的面積為S3,…,依次進行下去,最后記△P2005B2005P2006的面積為S2006,則S2006-S2005=查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com